1.基础概念

1.1 树

树(Tree） 是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:

1. 有且仅有一个特定的称为根(Root)的结点 ;

2. 当n>1时 , 其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn , 其中每一个集合本身又是一棵树 , 并且称为根的子树。

此外 , 树的定义还需要强调以下两点:

1. n>0时根结点是唯一的 , 不可能存在多个根结点 , 数据结构中的树只能有一个根结点。

2. m>0时 , 子树的个数没有限制 , 但它们一定是互不相交的。

1.2 节点

结点是数据结构中的基础 , 是构成复杂数据结构的基本组成单位。

1.3 节点的度

结点拥有的子树数目称为结点的度。

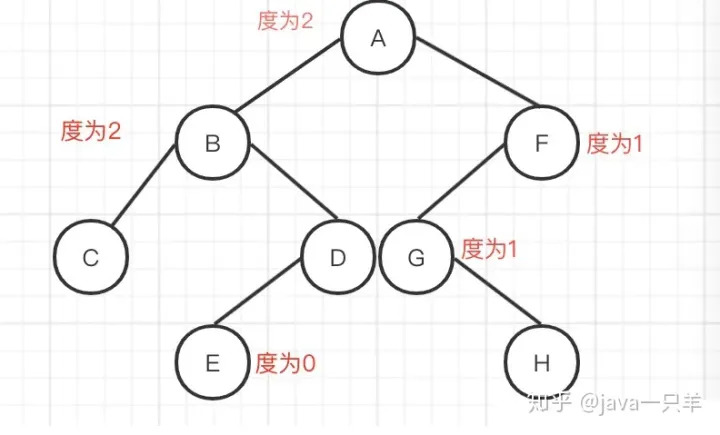
1.4 节点关系

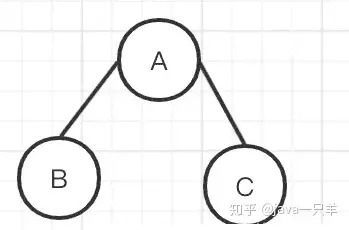
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。 同一个双亲结点的孩子结点之间互称兄弟结点。

• 如图 : A为B的双亲结点 , B为A的孩子结点。

• 结点B与结点C互为兄弟结点。

1.5 节点层次

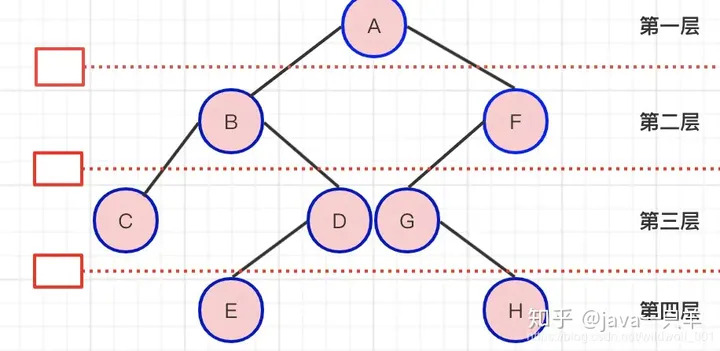
从根开始定义起 , 根为第一层 , 根的孩子为第二层 ,以此类推。

1.6 树的深度

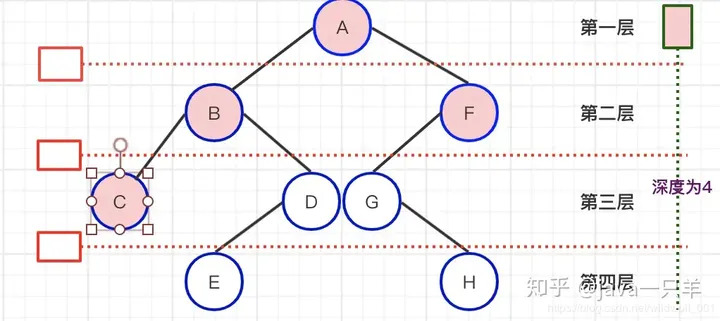
树中结点的最大层次数称为树的深度或高度。 如图树的深度为4。

2. 二叉树

二叉树是n(n>=0)个结点的有限集合 , 该集合或者为空集(称为空二叉树) ,或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

图解

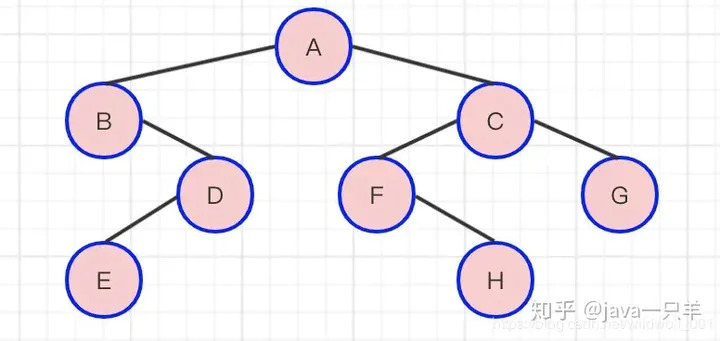
二叉树特点

由二叉树定义以及图示分析得出二叉树有以下特点:

1. 每个结点最多有两颗子树 , 所以二叉树中不存在度大于2的结点。

2. 左子树和右子树是有顺序的 , 次序不能任意颠倒。

3. 即使树中某结点只有一棵子树 , 也要区分它是左子树还是右子树。

二叉树性质

由二叉树定义以及图示分析得出二叉树有以下性质：

1. 在二叉树的第i层上最多有2^{i-1}个节点。(i>=1)

2. 二叉树中如果深度为k , 那么最多有2^{k-1}个节点。(k>=1)

3. n_0 =n_2 +1 。n_0 表示度数为0的节点, n_2表示度数为2的节点

性质 3 的计算方法为 : 对于一个二叉树来说 , 除了度为0的叶子结点和度为2的结点 , 剩下的就是度为1的结点(设为n_1) , 那么总结点n=n_0+n_1+n_2。 同时 , 对于每一个结点来说都是由其父结点分支表示的 , 假设树中分枝数为B , 那么总结点数 n=B+1。而分枝数是可以通过n_1和n_2 表示的，即B=n_1+2*n_2。所以 , n用另外一种方式表示为n=n_1+2*n_2+1。 两种方式得到的n值组成一个方程组 , 就可以得出n_0=n_2+1。

二叉树还可以继续分类 , 衍生出满二叉树和完全二叉树。

2.1 斜树

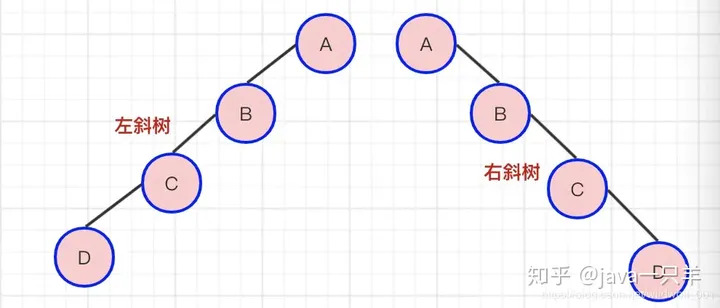
斜树 : 所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

2.2 平衡二叉树

平衡二叉查找树：简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树。它具有如下几个性质：

1. 可以是空树。

2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

平衡之意，如天平，即两边的分量大约相同。

平衡因子 : 某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子(BF,Balance Factor) , ,平衡二叉树中不存在平衡因子大于 1 的节点。

最小平衡二叉树 : 距离插入节点最近的 , 并且BF的绝对值大于1的节点为根节点的子树。旋转纠正只需要纠正最小不平衡子树即可。

平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式 , 左旋 与 右旋 。

旋转的目的就是减少高度 , 通过降低整棵树的高度来平衡。哪边的树高 , 就把那边的树向上旋转。

2.2.1 旋转方式

2.2.1.1 左旋

左旋配置规则如下:

• 旧根节点为新根节点的左子树

• 新根节点的左子树(如果存在)为旧根节点的右子树

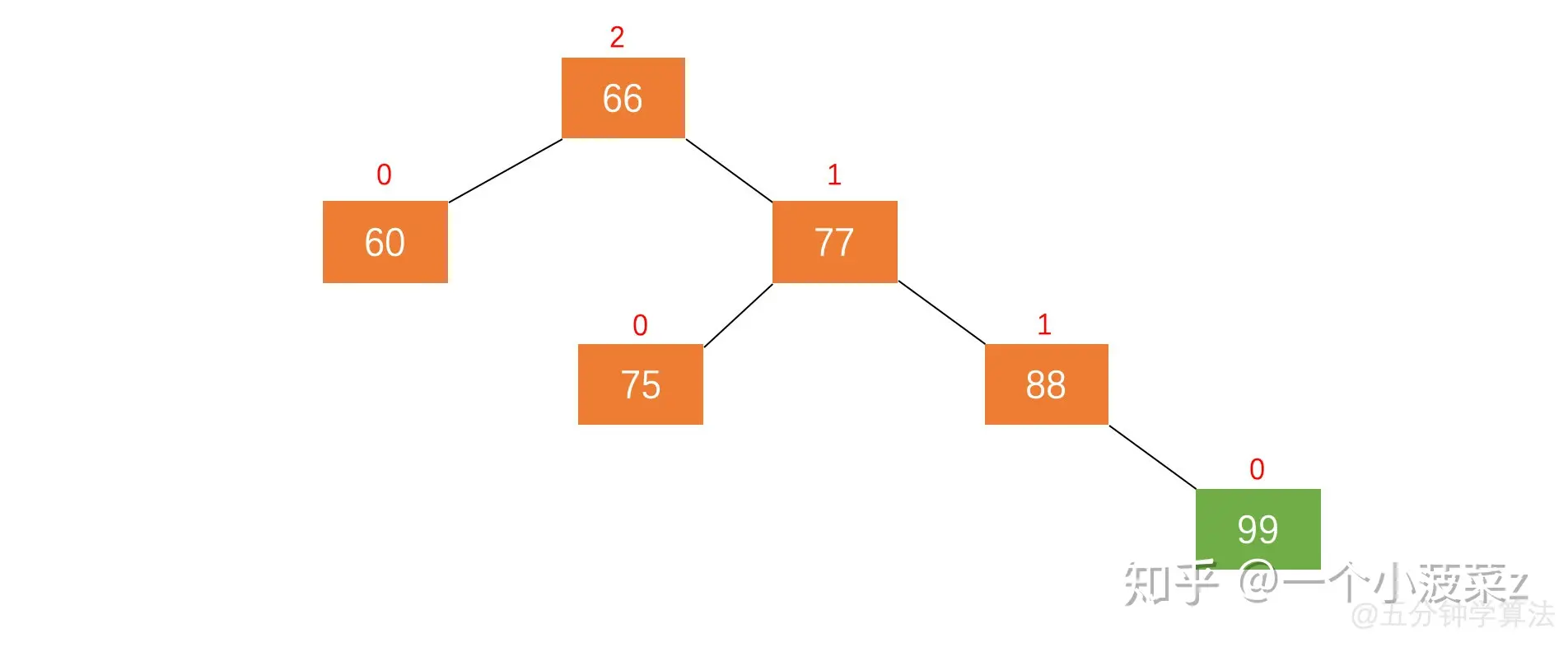
入新节点99后 , 节点66的左子树高度为1 , 右子树高度为3 , 此时平衡因子为-2。为保证树的平衡 , 此时需要对节点66做出旋转 , 因为右子树高度高于左子树 , 对节点进行左旋操作。流程如下:

1. 节点的右孩子替代此节点位置

2. 右孩子的左子树变为该节点的右子树

3. 节点本身变为右孩子的左子树

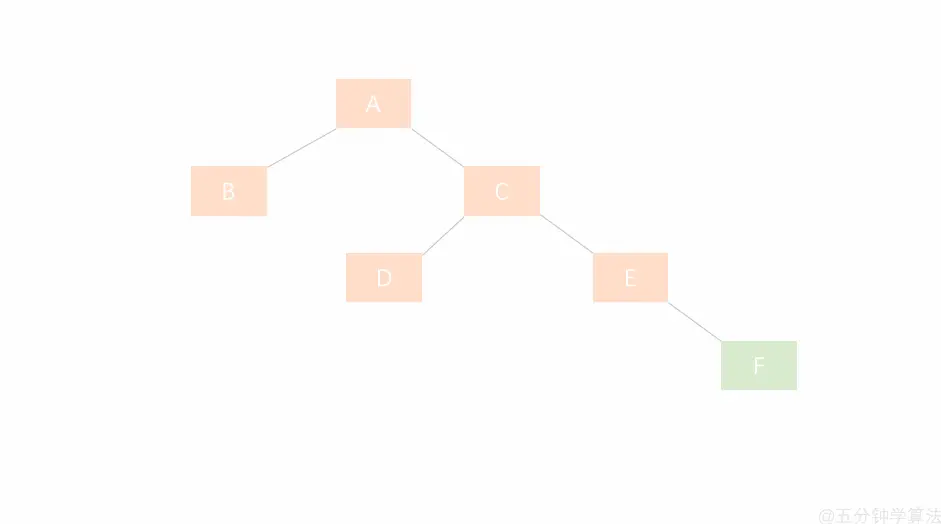
整个操作流程如下:

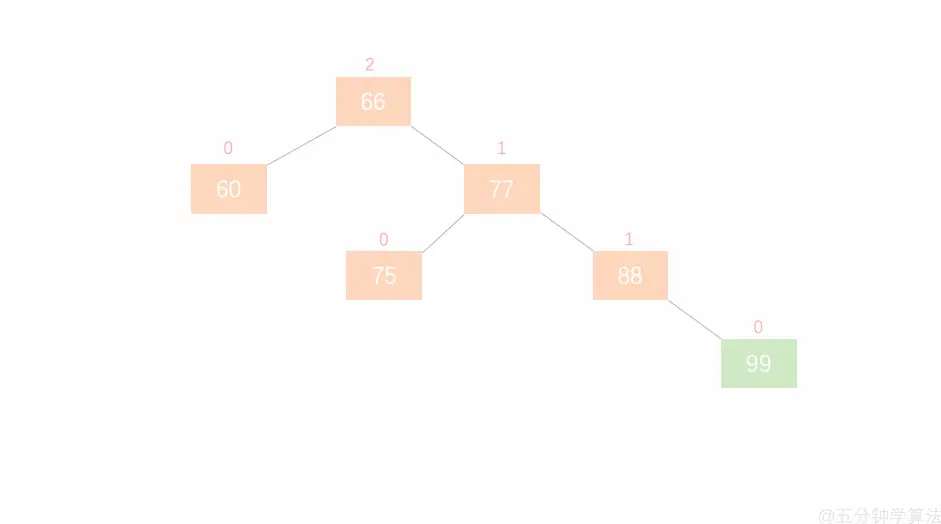
• 节点的右孩子替代此节点位置 —— 节点 66 的右孩子是节点 77 ，将节点 77 代替节点 66 的位置

• 右孩子的左子树变为该节点的右子树 —— 节点 77 的左子树为节点 75，将节点 75 挪到节点 66 的右子树位置

• 节点本身变为右孩子的左子树 —— 节点 66 变为了节点 77 的左子树

2.2.1.2 右旋

右旋配置规则如下:

• 旧根节点为新根节点的右子树

• 新根节点的右子树(如果存在)为旧根节点的左子树

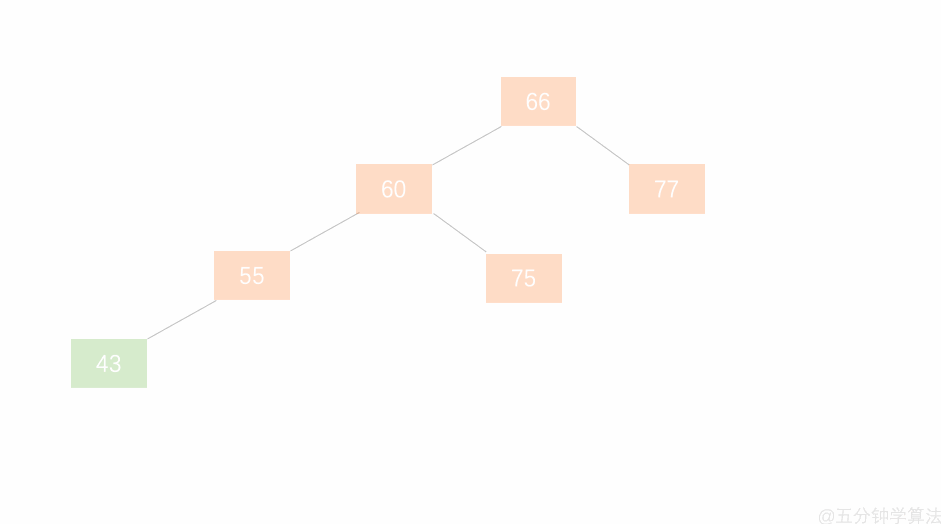
右旋操作与左旋类似 , 操作流程为:

1. 节点的左孩子代表此节点

2. 节点的左孩子的右子树变为节点的左子树

3. 将此节点作为左孩子节点的右子树。

2.2.2 四种插入方式

假设一颗 AVL 树的某个节点为A , 有四种操作会使 A 的左右子树高度差大于 1 , 从而破坏了原有 AVL 树的平衡性。平衡二叉树插入节点的情况分为以下四种：

2.2.2.1 A的左孩子的左子树插入节点(LL)

只需要执行一次右旋即可。

实现代码如下:

//LL型调整函数
//返回:新父节点
Tree LL_rotate(Tree node){
    //node为离操作结点最近的失衡的结点
    Tree parent=NULL,son;
    //获取失衡结点的父节点
    parent=node->parent;
    //获取失衡结点的左孩子
    son=node->lchild;
    //设置son结点右孩子的父指针
    if (son->rchild!=NULL)  son->rchild->parent=node;
    //失衡结点的左孩子变更为son的右孩子
    node->lchild=son->rchild;
    //更新失衡结点的高度信息
    update_depth(node);
    //失衡结点变成son的右孩子
    son->rchild=node;
    //设置son的父结点为原失衡结点的父结点
    son->parent=parent;
    //如果失衡结点不是根结点，则开始更新父节点
    if (parent!=NULL){
        //如果父节点的左孩子是失衡结点，指向现在更新后的新孩子son
        if (parent->lchild==node){
            parent->lchild=son;
        }else{
             //父节点的右孩子是失衡结点
              parent->rchild=son;
        }
     }
    //设置失衡结点的父亲
    node->parent=son;
    //更新son结点的高度信息
    update_depth(son);
    return son;
}

2.2.2.2 A的右孩子的右子树插入节点(RR)

只需要执行一次左旋即可。

实现代码如下:

//RR型调整函数
//返回新父节点
Tree RR_rotate(Tree node){
    //node为离操作结点最近的失衡的结点
    Tree parent=NULL,son;
    //获取失衡结点的父节点
    parent=node->parent;
    //获取失衡结点的右孩子
    son=node->rchild;
    //设置son结点左孩子的父指针
    if (son->lchild!=NULL){
          son->lchild->parent=node;
    }
    //失衡结点的右孩子变更为son的左孩子
    node->rchild=son->lchild;
    //更新失衡结点的高度信息
    update_depth(node);
    //失衡结点变成son的左孩子
    son->lchild=node;
    //设置son的父结点为原失衡结点的父结点
    son->parent=parent;
    //如果失衡结点不是根结点，则开始更新父节点
    if (parent!=NULL){
        //如果父节点的左孩子是失衡结点，指向现在更新后的新孩子son
        if (parent->lchild==node){
            parent->lchild=son;
        }else{
            //父节点的右孩子是失衡结点
            parent->rchild=son;
        } 
    }
    //设置失衡结点的父亲
    node->parent=son;
    //更新son结点的高度信息
    update_depth(son);
    return son;
}

2.2.2.3 A的左孩子的右子树插入节点(LR)

若 A 的左孩子节点 B 的右子树 E 插入节点 F , 导致节点A 失衡 , 如图:

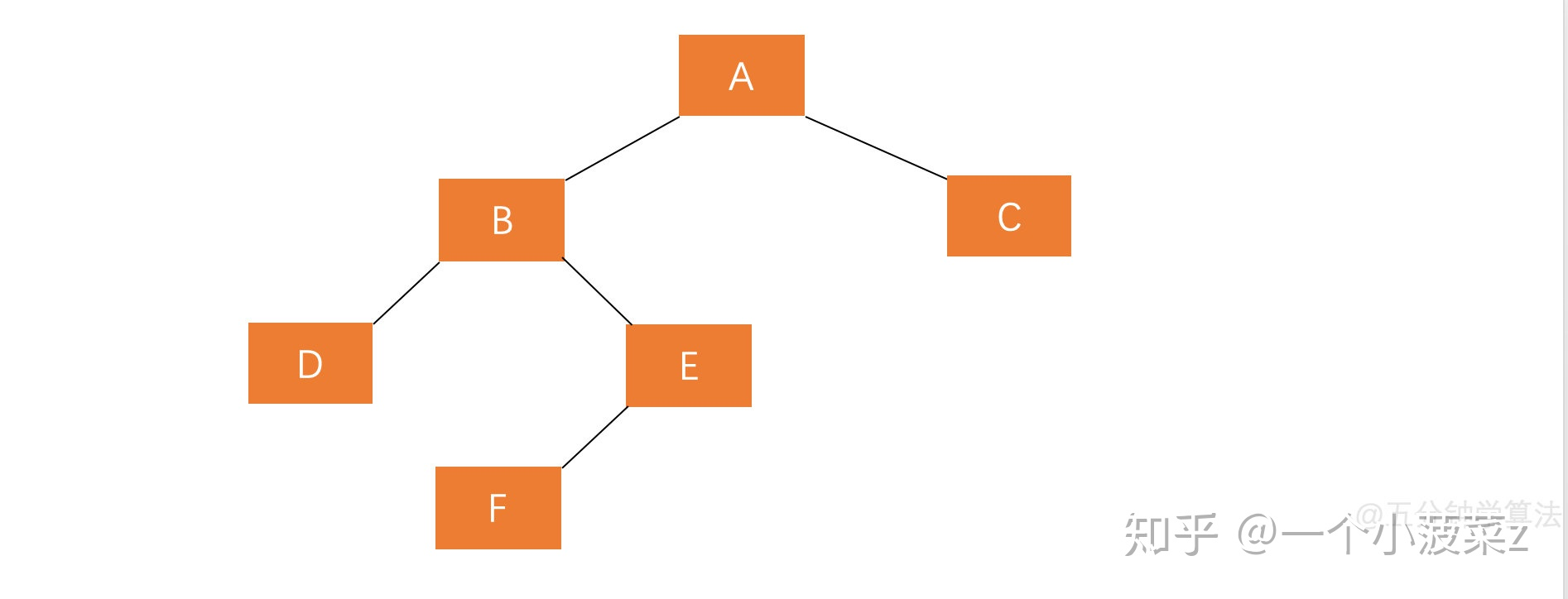
A 的平衡因子为2 , 若仍按照右旋调整 , 则变化后的图形为这样:

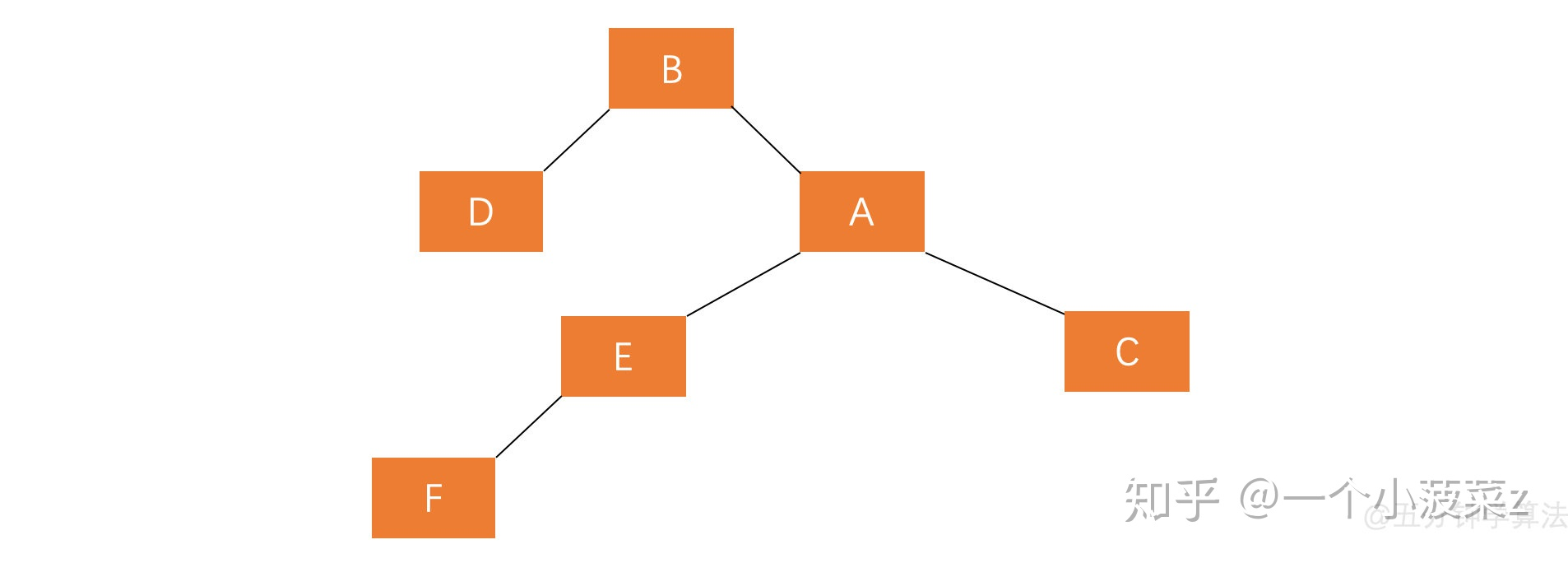
经过右旋调整发现 ; 调整后树仍然失衡，说明这种情况单纯的进行右旋操作不能使树重新平衡。那么这种插入方式需要执行两步操作，使得旋转之后为 原来根结点的左孩子的右孩子作为新的根节点 。

1. 对失衡节点 A 的左孩子 B 进行左旋操作 , 即上述RR情形操作。

2. 对失衡节点A做右旋操作 , 即上述LL情形操作。

调整过程如下:

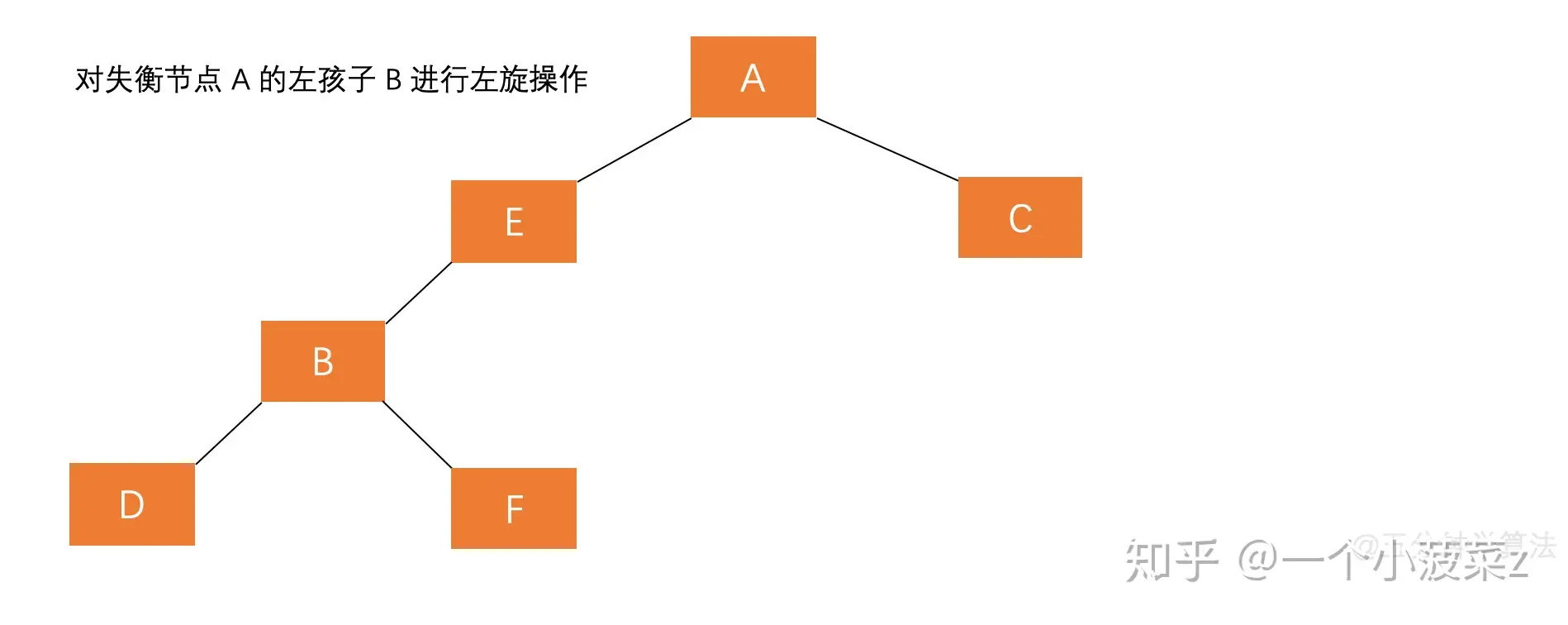
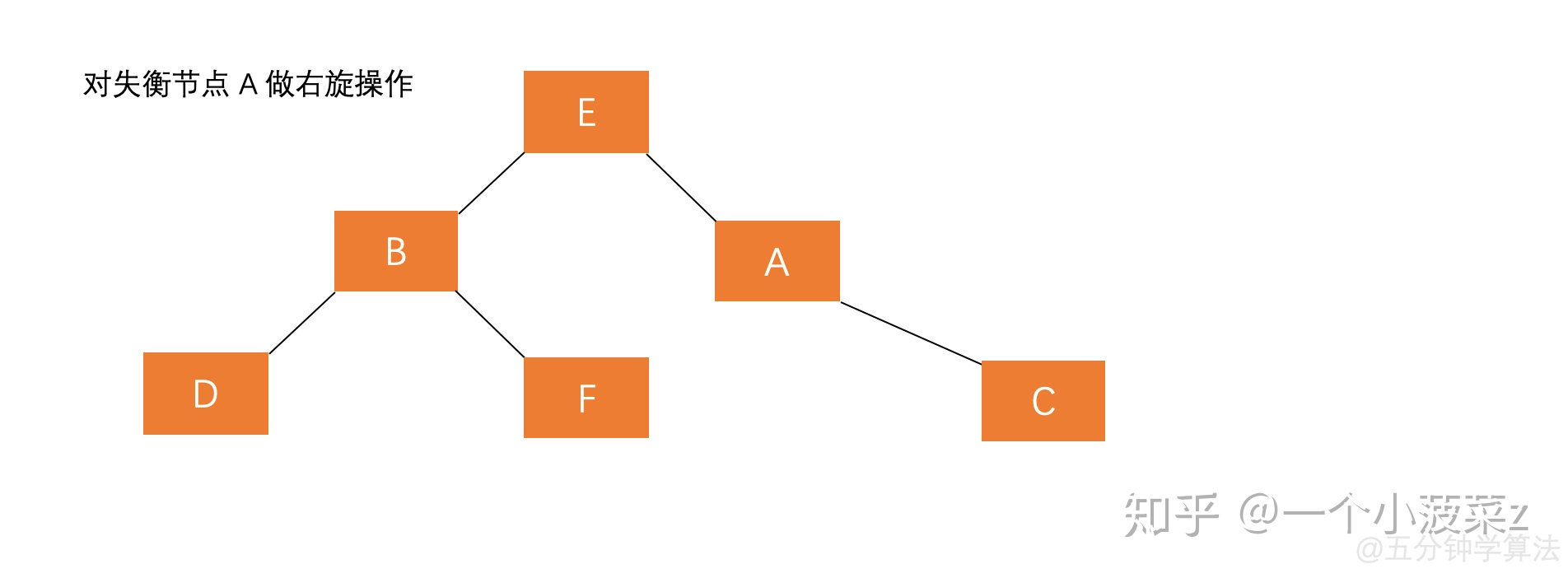
也就是说，经过这两步操作，使得 原来根节点的左孩子的右孩子 E 节点成为了新的根节点。

代码实现:

//LR型，先左旋转，再右旋转
//返回：新父节点
Tree LR_rotate(Tree node){
    RR_rotate(node->lchild);
    return LL_rotate(node);
}

2.2.2.4 A的右孩子的左子树插入节点(RL)

右孩子插入左节点的过程与左孩子插入右节点过程类似 , 也是需要执行两步操作 , 使得旋转之后为 原来根节点的右孩子的左孩子作为新的根节点。

1. 对失衡节点 A 的右孩子 C 进行右旋操作 , 即上述LL情形操作。

2. 对失衡节点 A 做左旋操作 , 即上述RR情形操作。

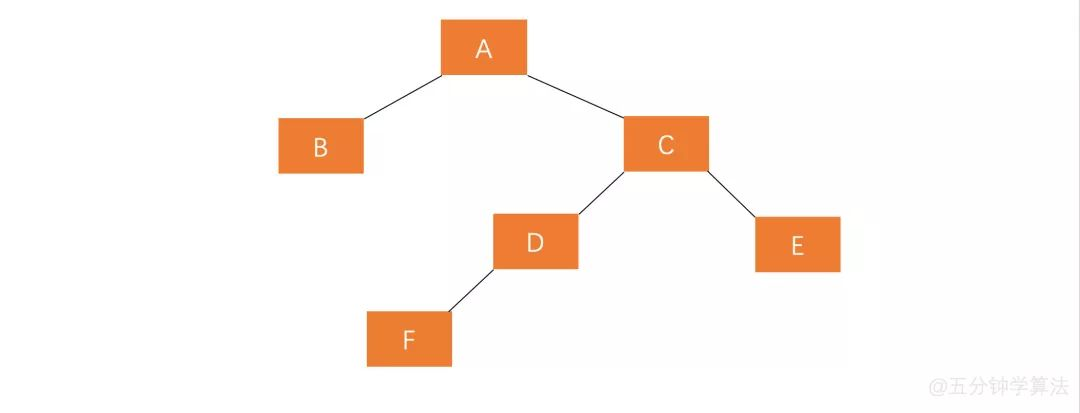
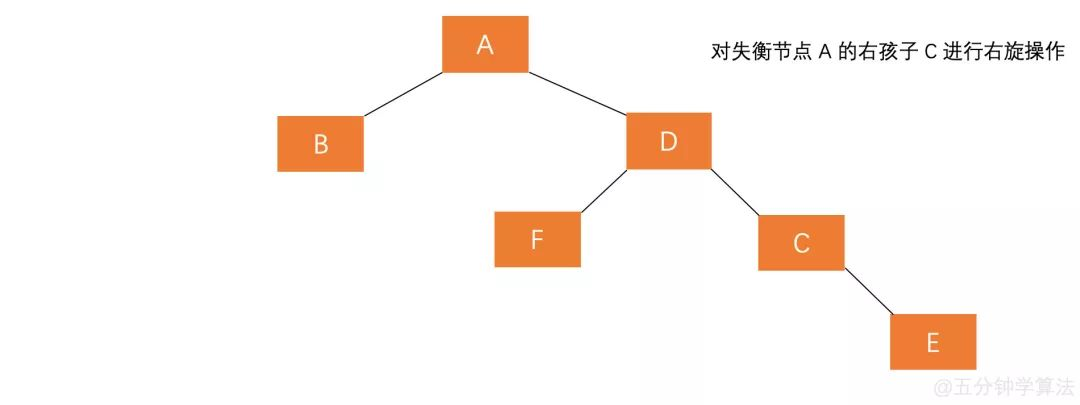
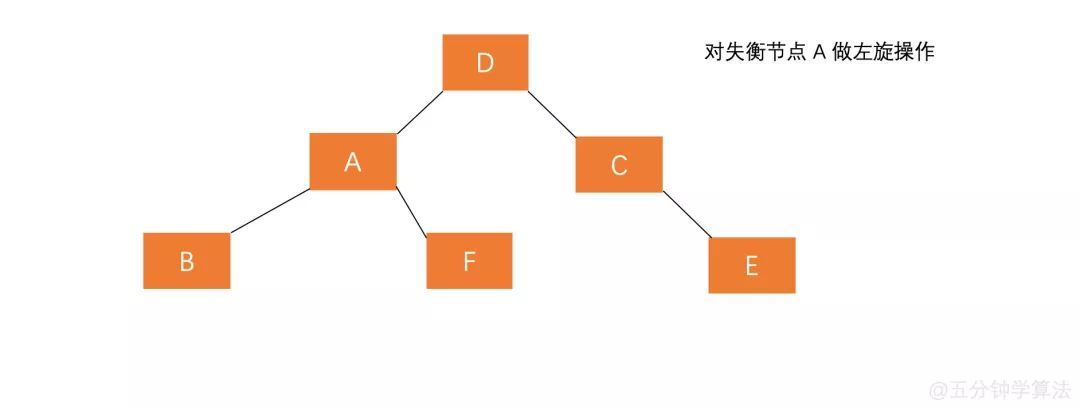
也就是说 , 经过这两步操作，使得 原来根节点的右孩子的左孩子 D 节点成为了新的根节点。

代码实现：

//RL型，先右旋转，再左旋转
//返回:新父节点
Tree RL_rotate(Tree node){
    LL_rotate(node->rchild);
    return RR_rotate(node);
}

补充：

上述四种插入方式的代码实现的辅助代码如下:

//更新当前深度
void update_depth(Tree node){
    if (node==NULL){
        return;
    }else{
        int depth_Lchild=get_balance(node->lchild); //左孩子深度
        int depth_Rchild=get_balance(node->rchild); //右孩子深度
        node->depth=max(depth_Lchild,depth_Rchild)+1;
    }
}
​
//获取当前节点的深度
int get_balance(Tree node){
    if (node==NULL){
         return 0;
    }
    return node->depth;
}
​
//返回当前平衡因子
int is_balance(Tree node){
    if (node==NULL){
         return 0;
    }else{
         return get_balance(node->lchild)-get_balance(node->rchild); 
    }
}

2.2.3 AVL树的四种删除节点方式

AVL 树和二叉查找树的删除操作情况一致 , 都分为四种情况：

1. 删除叶子节点

2. 删除的节点只有左子树

3. 删除的节点只有右子树

4. 删除的节点既有左子树又有右子树

只不过AVL树在删除节点后需要重新检查平衡性并修正 , 同时 , 删除操作与插入操作后的平衡修正区别在于 ,插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正 , 而删除操作需要修正栈中的所有非平衡节点。

删除操作的大致步骤如下：

• 以前三种情况为基础尝试删除节点，并将访问节点入栈。

• 如果尝试删除成功 , 则依次检查栈顶节点的平衡状态 ,遇到非平衡节点 , 即进行旋转平衡 , 直到栈空。

• 如果尝试删除失败 , 证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它 , 将访问节点继续入栈。

• 再依次检查栈顶节点的平衡状态和修正直到栈空。

对于删除操作造成的非平衡状态的修正 , 可以这样理解: 对左或者右子树的删除操作相当于对右或者左子树的插入操作 , 然后再对应上插入的四种情况选择相应的旋转就好了。

2.2.3.1 删除叶子节点

处理步骤:

1. 将该节点直接从树中删除;

2. 其父节点的子树高度的变化将导致父节点平衡因子的变化 , 通过向上检索并推算其父节点是否失衡 ;

3. 如果其父节点未失衡 , 则继续向上检索推算其父节点的父节点是否失衡…如此反复2的判断，直到根节点 ；如果向上推算过程中发现了失衡的现象，则进行 ④ 的处理；

4. 如果其父节点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根节点的树的高度发生变化，则继续进行 ② 的检索推算；如果与原来以父节点为根节点的高度一致时，则可说明父节点的父节点及祖先节点的平衡因子将不会有变化，因此可以退出处理;

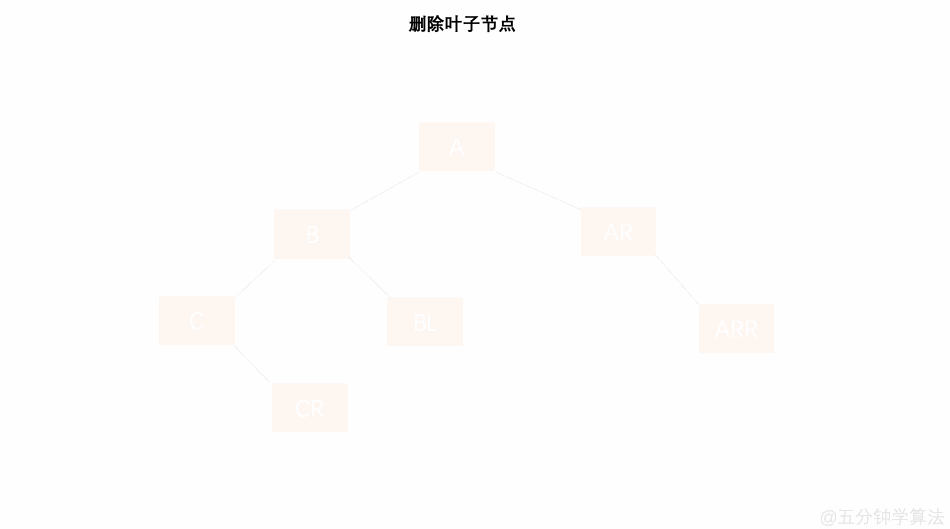
具体数字演示:

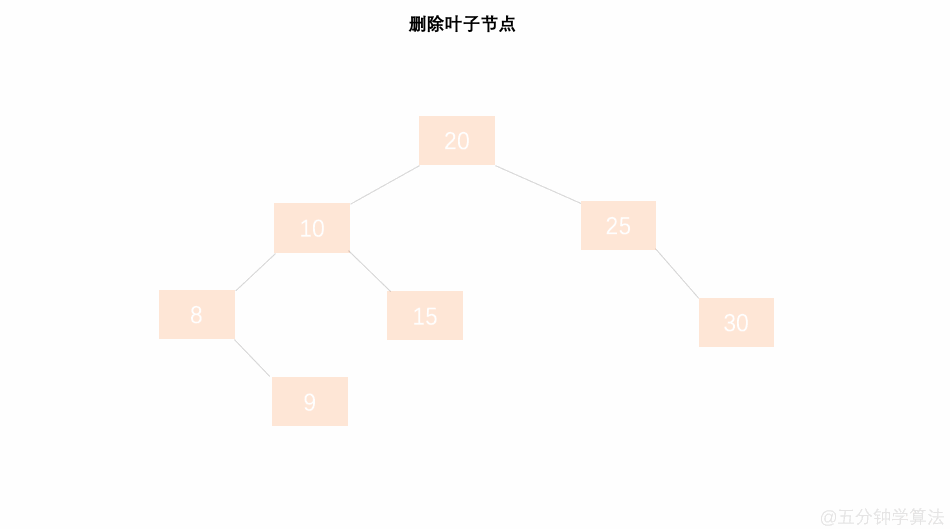
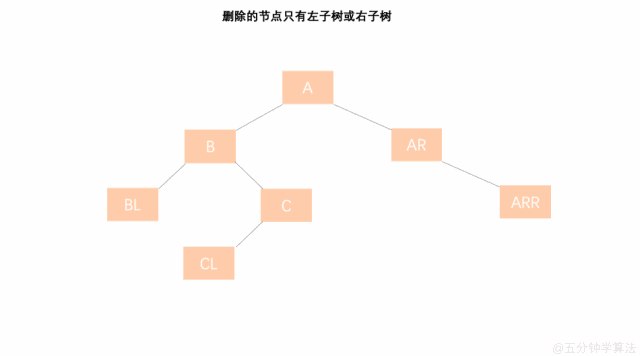
2.2.3.2 删除的节点只有左子树或右子树

处理步骤：

1. 将左子树（右子树）替代原有节点 C 的位置；

2. 节点 C 被删除后，则以 C 的父节点 B 为起始推算点，依此向上检索推算各节点（父、祖先）是否失衡；

3. 如果其父节点未失衡，则继续向上检索推算其父节点 的父节点 是否失衡…如此反复 ② 的判断，直到根节点 ；如果向上推算过程中发现了失衡的现象，则进行 ④ 的处理；

4. 如果其父节点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根节点的树的高度发生变化，则继续进行 ② 的检索推算；如果与原来以父节点为根节点的高度一致时，则可说明父节点的父节点及祖先节点的平衡因子将不会有变化，因此可以退出处理；

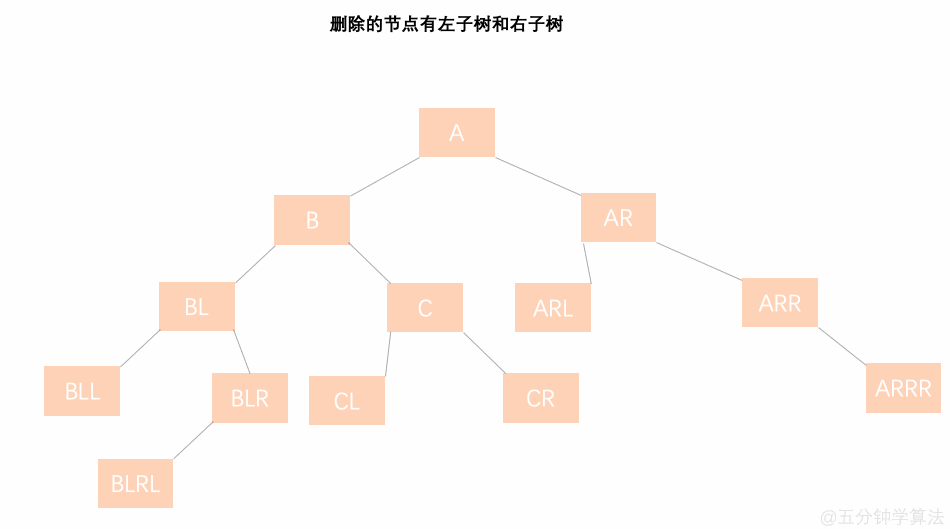
2.2.3.3 删除的节点既有左子树又有右子树

处理步骤：

①、找到被删节点 B 和替代节点 BLR (节点 B 的前继节点或后继节点 —— 在此选择 前继)；

②、将替代节点 BLR 的值赋给节点 B ，再把替代节点 BLR 的左孩子 BLRL 替换替代节点 BLR 的位置；

③、以 BLR 的父节点 BL 为起始推算点，依此向上检索推算父节点或祖先节点是否失衡；

④、如果其父节点未失衡，则继续向上检索推算其父节点的父节点是否失衡…如此反复③的判断，直到根节点；如果向上推算过程中发现了失衡的现象，则进行⑤的处理；

⑤、如果其父节点失衡，则判断是哪种失衡类型 [LL、LR、RR、RL] ，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根节点的树的高度发生变化，则继续进行 ② 的检索推算；如果与原来以父节点为根节点的高度一致时，则可说明父节点的父节点及祖先节点的平衡因子将不会有变化，因此可以退出处理；

注：在这里，小吴并没有给出AVL的删除操作的代码 , 也没有给出平衡性修复的动画，因为我并不打算过多去讨论它，更复杂的删除操作过程将放在后续的 红黑树 中进行讨论。

2.3 红黑树

红黑树和平衡二叉树类似 , 本质上都是为了解决排序二叉树在极端情况下退化成链表导致检索效率大大降低的问题 , 红黑树最早是由Rudolf Bayer于1972年发明的。

红黑树首先肯定是一个排序二叉树 , 它在每个节点上增加了一个存储位来表示节点的颜色，可以是RED或BLACK 。

• 性质1 : 每个节点要么是红色 , 要么是黑色。

• 性质2 : 根节点永远是黑色的。

• 性质3 : 所有的叶子节点都是空节点(即null) , 并且是黑色的。

• 性质4 : 每个红色节点的两个子节点都是黑色。(从每个叶子到根的路径上不会有两个连续的红色节点。)

• 性质5 : 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

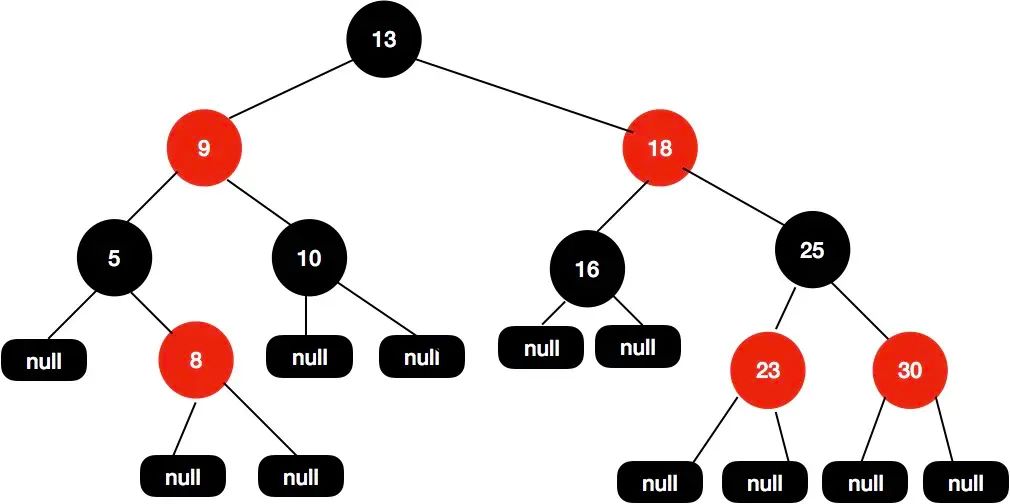
针对上面的5种性质 , 我们简单理解下 , 对于性质 1 和性质2 , 相当于是对红黑树每个节点的约束 , 根节点是黑色 , 其他的节点要么是红色 , 要么是黑色。

对于性质 3 中指定红黑树的每个叶子节点都是空节点 , 而且叶子节点都是黑色 , 但Java实现的红黑树会使用null来代表空节点 , 因此我们在遍历Java里的红黑树的时候会看不到叶子节点 , 而看到的是每个叶子节点都是红色的 , 这一点需要注意。

对于性质5 , 这里我们需要注意的是 , 这里的描述是从任一节点 , 从任一节点到它的子树的每个叶子节点黑色节点的数量都是相同的 , 这个数量被称为这个节点的黑高。

如果我们从根节点出发到每个叶子节点的路径都包含相同数量的黑色节点 , 这个黑色节点的数量被称为树的黑色高度。树的黑色高度和节点的黑色高度是不一样的，这里要注意区分。

其实到这里有人可能会问了 , 红黑树的性质说了一大堆 , 那是不是说只要保证红黑树的节点是红黑交替就能保证树是平衡的呢?

其实不是这样的 , 我们可以看来看下面这张图 :

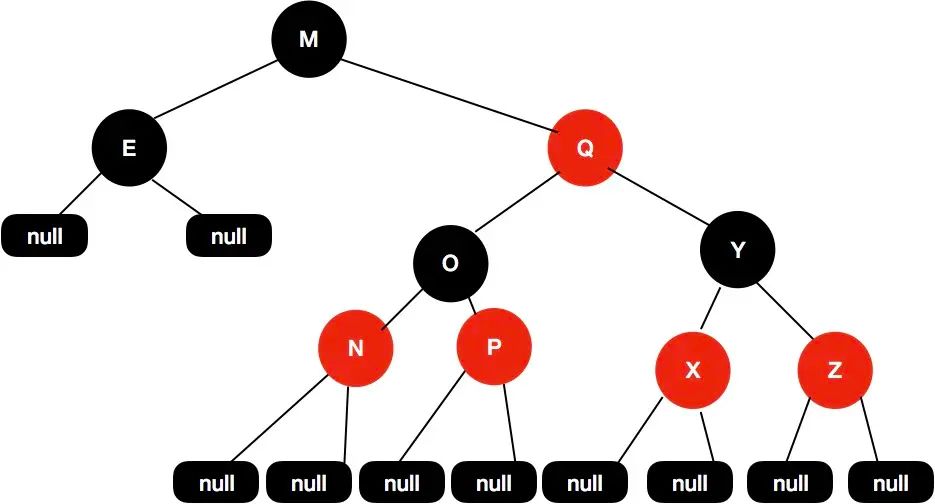
左边的子树都是黑色节点 , 但是这个红黑树依然是平衡的 , 5条性质它都满足。

这个树的黑色高度为3 , 从根节点到叶子节点的最短路径长度是2 , 该路径上全是黑色节点 , 包括叶子节点 , 从根节点到叶子节点最长路径为4 , 每个黑色节点之间会插入红色节点。

通过上面的性质4和性质5 , 其实上保证了没有任何一条路径会比其他路径长出两倍 , 所以这样的红黑树是平衡的。

其实这算是一个推论 , 红黑树在最差情况下 , 最长的路径都不会比最短的路径长出两倍。其实红黑树并不是真正的平衡二叉树 , 它只能保证大致是平衡的 , 因为红黑树的高度不会无限增高 , 在实际应用中 , 红黑树的统计性能要高于平衡二叉树 , 但极端性能略差。

2.3.1 红黑树插入

想要彻底理解红黑树 , 除了上面说到的理解红黑树的性质以外 , 就是理解红黑树的插入操作了。

红黑树的插入和普通排序二叉树的插入基本一致 , 排序二叉树的要求是左子树上的所有节点都要比根节点小 , 右子树上的所有节点都要比跟节点大 , 当插入一个新的节点的时候 , 首先要找到当前要插入的节点适合放在排序二叉树哪个位置 , 然后插入当前节点即可。红黑树和排序二叉树不同的是 , 红黑树需要在插入节点调整树的结构来让树保持平衡。

一般情况下 , 红黑树中新插入的节点都是红色的 , 那么 , 为什么说新加入到红黑树中的节点要是红色的呢?

这个问题可以这样理解 , 我们从性质5中知道 , 当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的，此时假如新的黑色节点的话，必然破坏规则，但加入红色节点却不一定，除非其父节点就是红色节点，因此加入红色节点，破坏规则的可能性小一些。

接下来我们重点来讲红黑树插入新节点后是如何保持平衡的。

给定下面这样一颗红黑树:

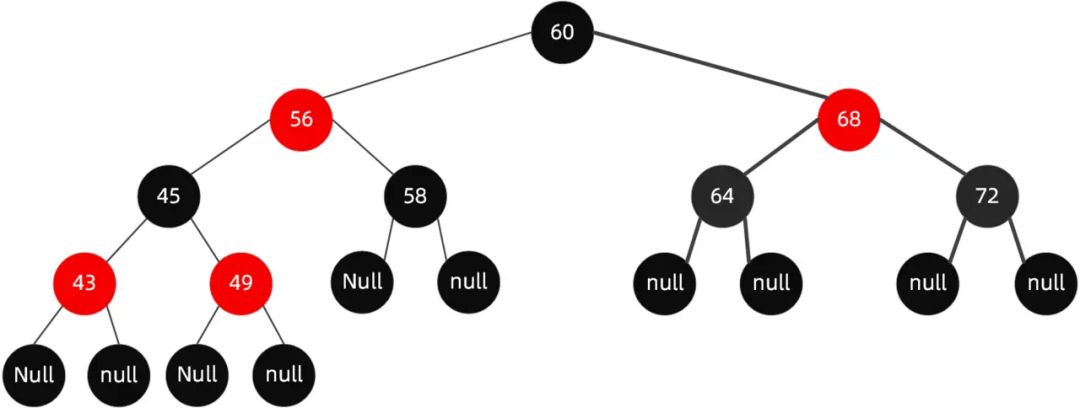
当我们插入值为66的节点的时候 , 示意图如下:

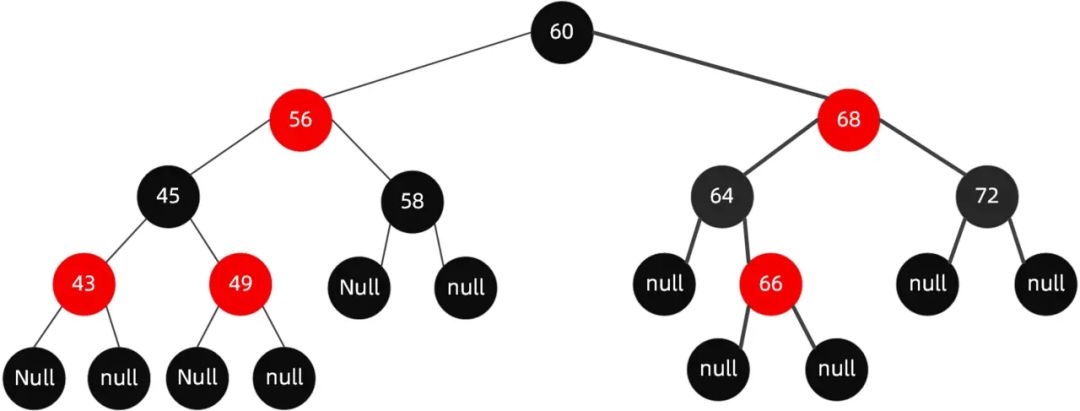
很明显 , 这个时候结构依然遵循着上述5大特性 , 无需启动自动平衡机制调整节点平衡状态。

如果再向里面插入值为51的节点呢，这个时候红黑树变成了这样。

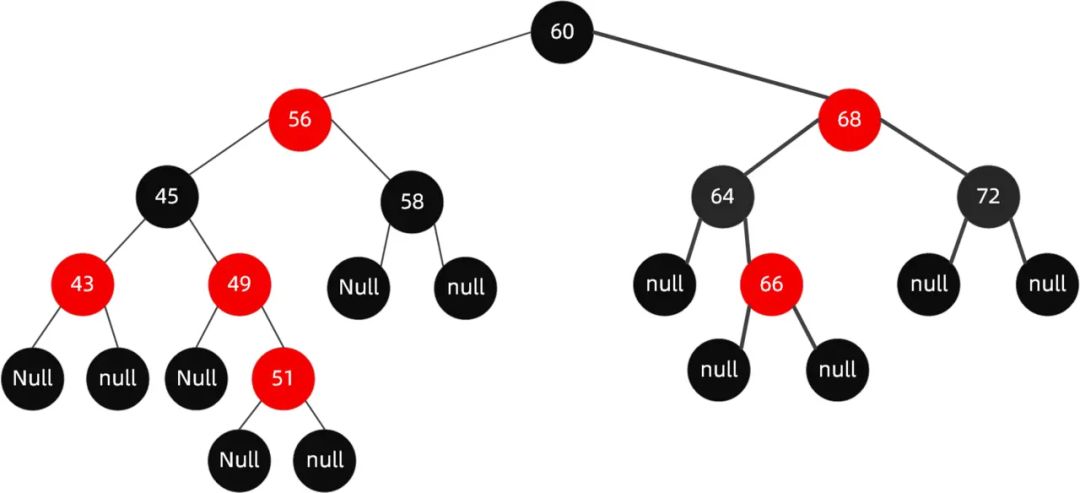
这样的结构实际上是不满足性质4的 , 红色两个子节点必须是黑色的 , 而这里49这个红色节点现在有个51的红色节点与其相连。

这个时候我们需要调整这个树的结构来保证红黑树的平衡。

首先尝试将49这个节点设置为黑色 , 如下示意图。

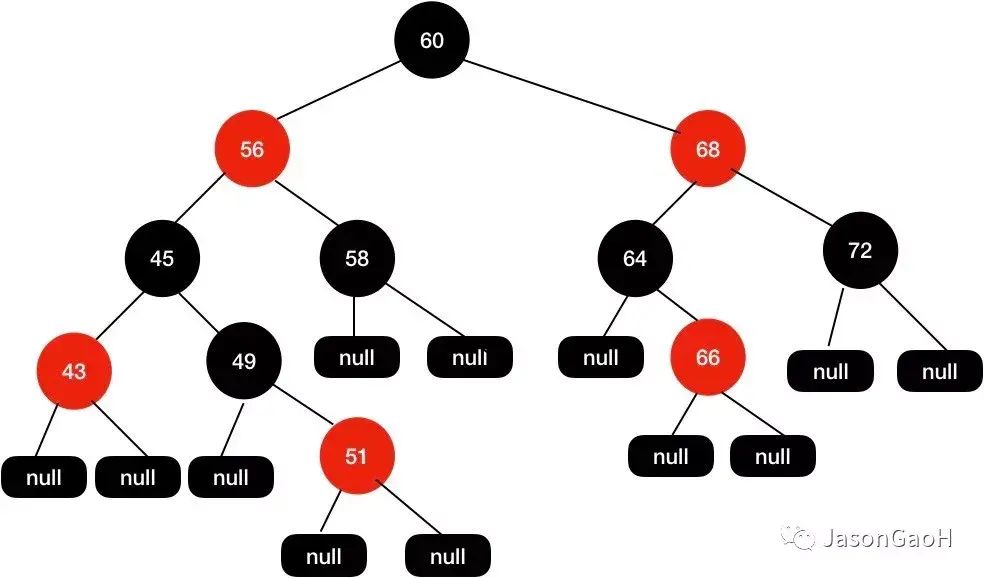
这个时候我们发现黑高是不对的 , 其中60-56-45-49-51-null这条路径有 4 个黑节点 , 其他路径的黑色节点是 3 个。

接着调整红黑树 , 我们再次尝试把45这个节点设置为红色的 , 如下图所示:

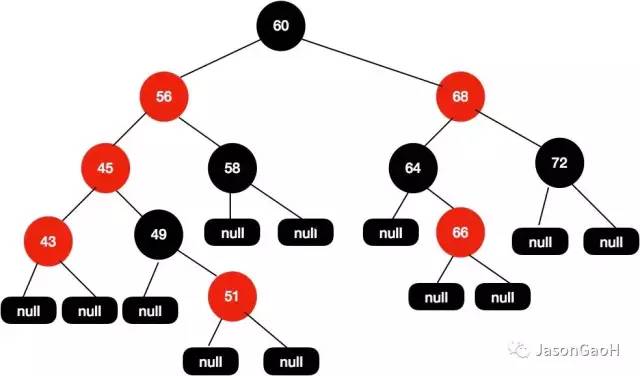
这个时候我们发现问题又来了 , 56-45-43都是红色节点的 , 出现了红色节点相连的问题。

于是我们需要再把 56 和 43 设置为黑色的 , 如下图所示。

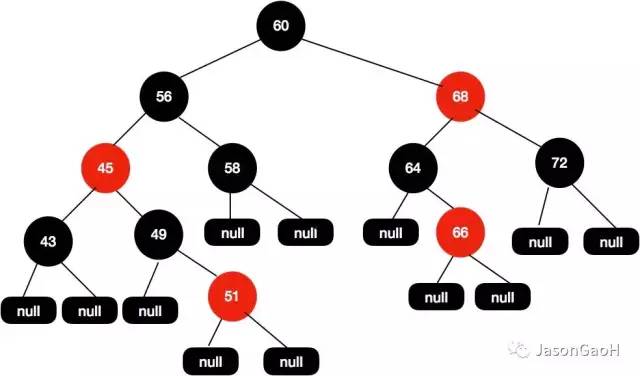
于是我们把 68 这个红色节点设置为黑色的。

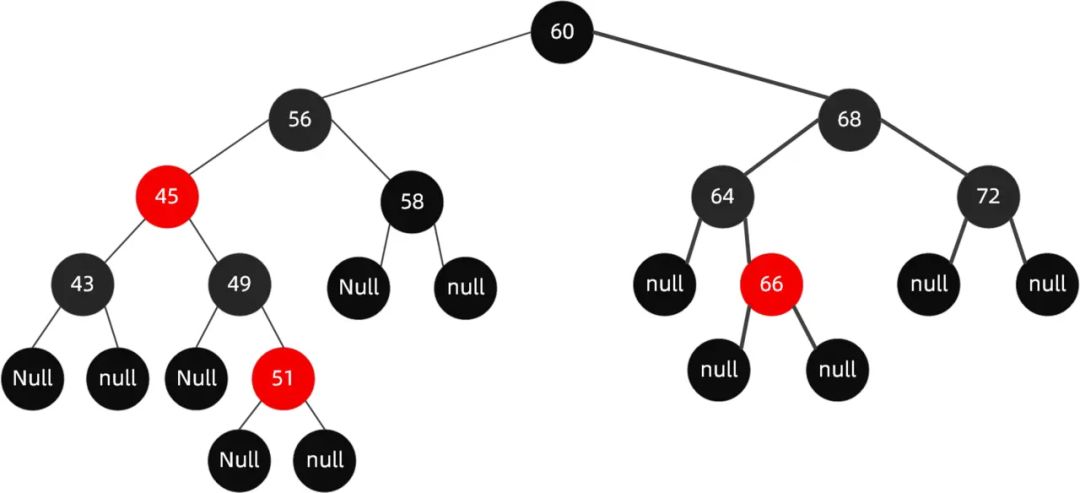
对于这种红黑树插入节点的情况下 , 我们可以只需要通过变色就可以保持树的平衡了。但是并不是每次都是这么幸运的 , 当变色行不通的时候 , 我们需要考虑另一个手段就是旋转了。

例如下面这种情况 , 同样还是拿这颗红黑树举例。

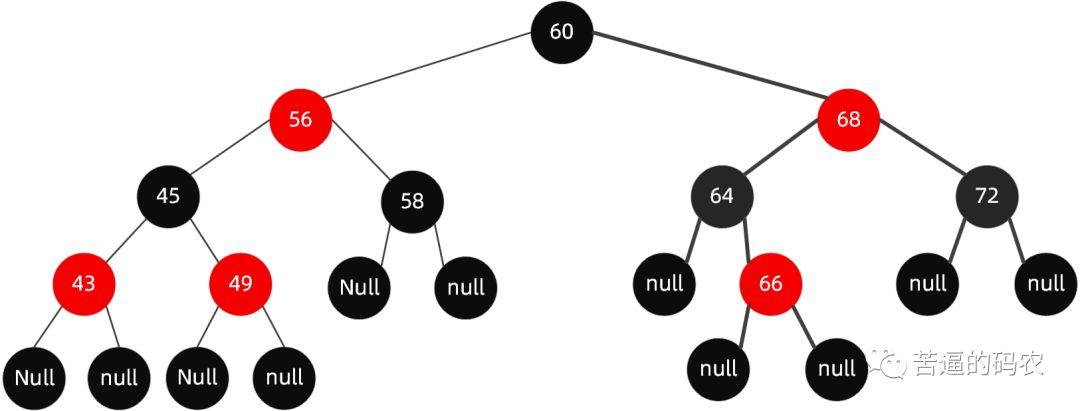
现在这颗红黑树，我们现在插入节点65。

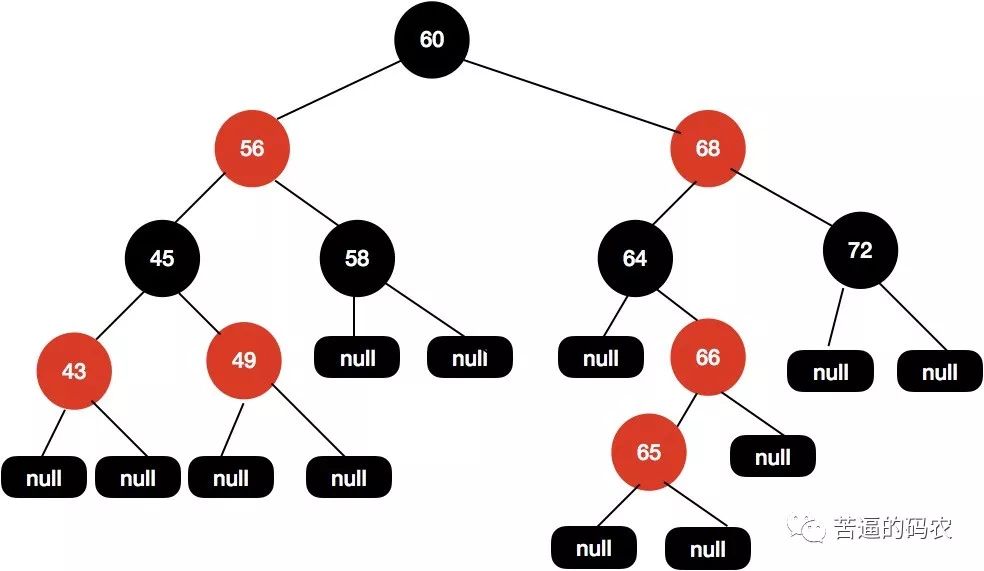
我们尝试把 66 这个节点设置为黑色 , 如下图所示。

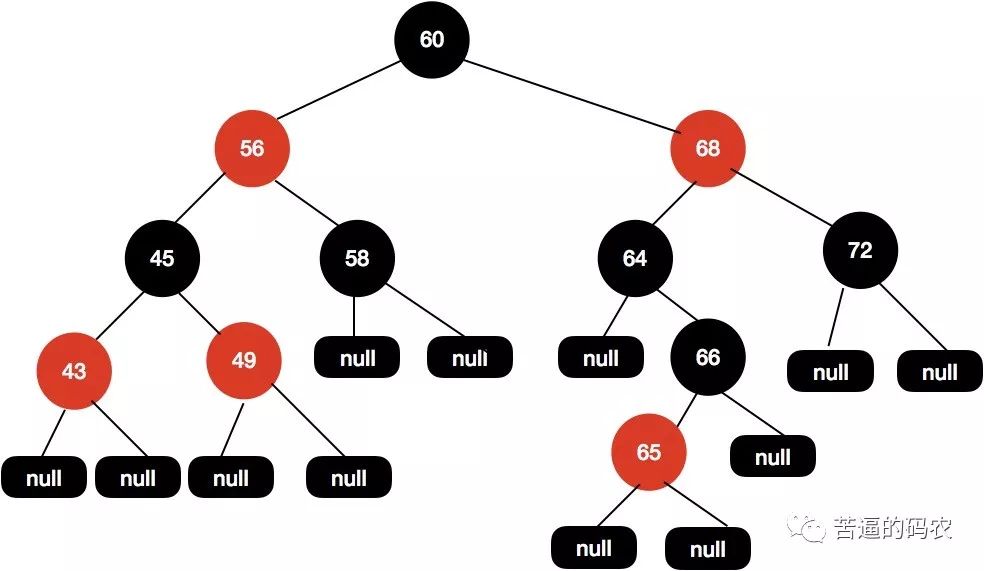
这样操作之后黑高又出现不一致的情况了, 60-68-64-null 有 3 个黑色节点 , 而60-68-64-66-null 这条路径有 4 个黑色节点 , 这样的结构是不平衡的。

或者我们把 68 设置为黑色 , 把 64 设置为红色 , 如下图所示:

但是 , 同样的问题 , 上面这颗红黑树的黑色高度还是不一致 , 60-68-64-null 和 60-68-64-66-null 这两条路径黑色高度还是不一致。

这种情况如果只通过变色的情况是不能保持红黑树的平衡的。

2.3.2 红黑树旋转

接下来我们讲讲红黑树的旋转 , 旋转分为左旋和右旋。

2.3.2.1 左旋

文字描述 : 逆时针旋转两个节点 , 让一个节点被其右子节点取代 , 而该节点成为右子节点的左子节点。

文字描述太抽象 , 接下来看下图片展示。

首先断开节点PL与右子节点G的关系 , 同时将其右子节点的引用指向节点C2 ; 然后断开节点G与左子节点C2的关系 , 同时将G的左子节点的应用指向节点PL。

接下来再放下gif图 , 希望能帮助大家更好地理解左旋 , 图片来自网络。

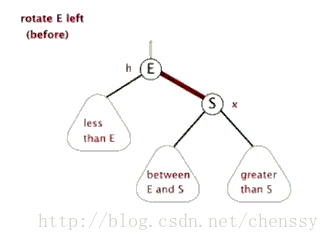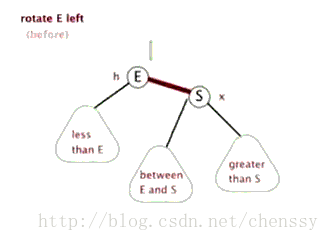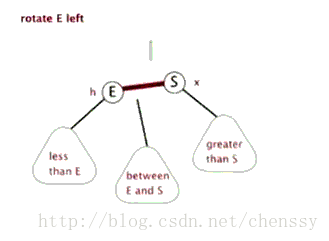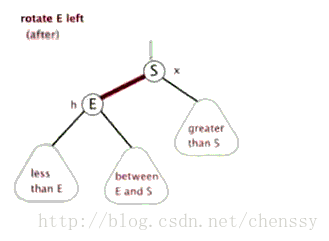
2.3.2.2 右旋

文字描述 : 顺时针旋转两个节点 , 让一个节点被其左子节点取代 , 而该节点成为左子节点的右子节点。

右旋的图片展示 :

首先断开节点G与左子节点PL的关系 , 同时将其左子节点的引用指向节点C2 ; 然后断开节点PL与右子节点C2的关系 , 同时将PL的右子节点的应用指向节点G。

右旋的gif展示(图片来自网络):

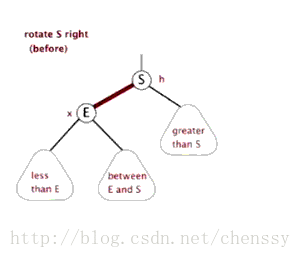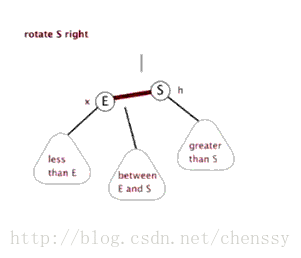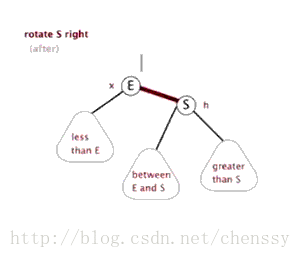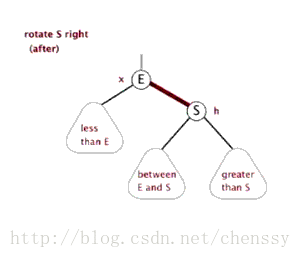
介绍完了左旋和右旋基本操作 , 我们来详细介绍下红黑树的几种旋转场景。

左左节点旋转( 插入节点的父节点是左节点 , 插入节点也是左节点)

如下图所示的红黑树 , 我们插入节点是65。

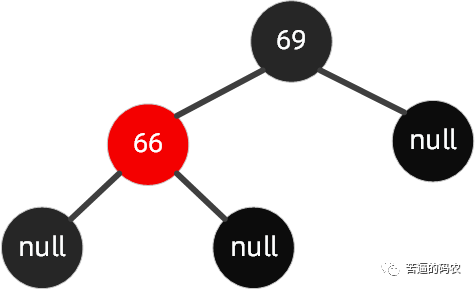
操作步骤如下可以围绕祖父节点 69 右旋 , 再结合变色 , 步骤如下所示:

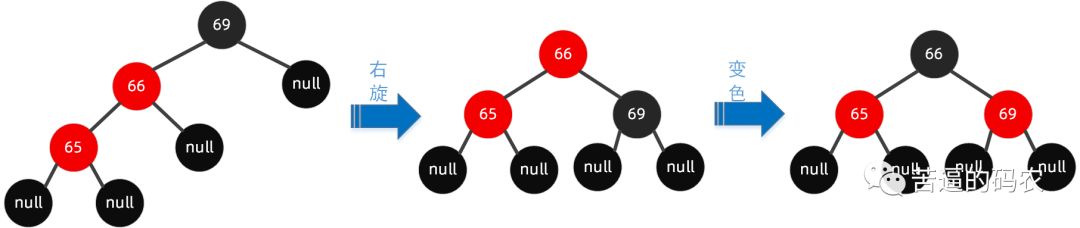
左右节点旋转( 插入节点的父节点是左节点 , 插入节点是右节点)

还是上面这颗红黑树 , 我们再插入节点67 。

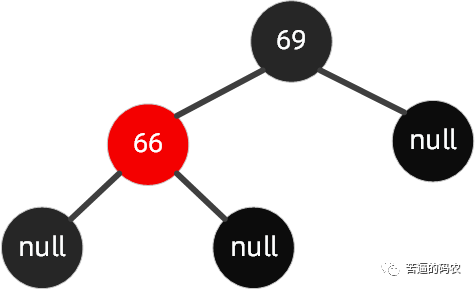
这种情况我们可以这样操作 , 先围绕父节点 66 左旋 , 然后再围绕祖父节点69右旋 , 最后再将 67 设置为黑色 , 把69设置为红色 , 如下图所示。

右左节点旋转( 插入节点的父节点是右节点 , 插入节点左节点)

如下图这种情况 , 我们要插入节点68。

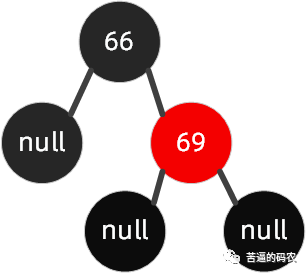
这种情况 , 我们可以先围绕父节点69右旋 , 接着再围绕祖父节点 66 左旋 , 最后把 68节点设置为黑色 , 把66设置为红色 , 我们的具体操作步骤如下所示。

右右节点旋转( 插入节点的父节点是右节点 , 插入节点也是右节点)

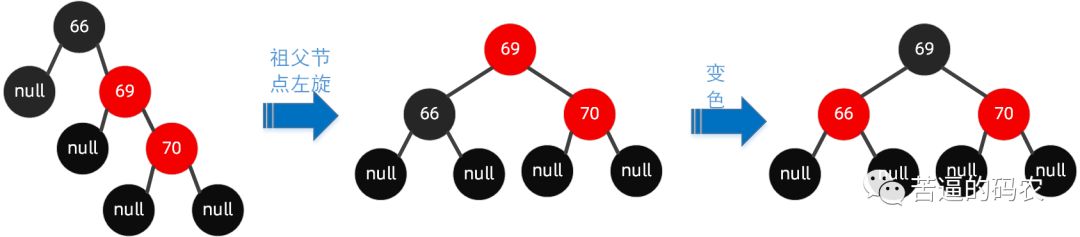
还是来上面的图来举例 , 我们在这颗红黑树上插入节点70 。

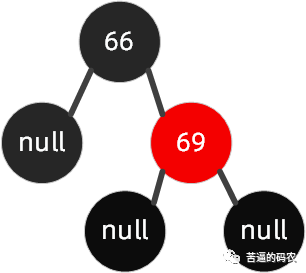
我们可以这样操作围绕祖父节点 66左旋 , 再把旋转后的根节点69设置为黑色 , 把66这个节点设置为红色。具体可以参看下图:

2.3.3 红黑树的代码实现以及代码详解(Java)

Java中的红黑树实现类是TreeMap , 接下来我们尝试从源码角度来逐行解释TreeMap这一套机制是如何运作的。

// TreeMap中使用Entry来描述每个节点
 static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
        Entry<K,V> left;
        Entry<K,V> right;
        Entry<K,V> parent;
        boolean color = BLACK;
        ...
 }

TreeMap的put方法。

 public V put(K key, V value) {
        //先以t保存链表的root节点
        Entry<K,V> t = root;
        //如果t=null,表明是一个空链表，即该TreeMap里没有任何Entry作为root
        if (t == null) {
            compare(key, key); // type (and possibly null) check
            //将新的key-value创建一个Entry，并将该Entry作为root
            root = new Entry<>(key, value, null);
            size = 1;
            //记录修改次数加1
            modCount++;
            return null;
        }
        int cmp;
        Entry<K,V> parent;
        // split comparator and comparable paths
        Comparator<? super K> cpr = comparator;
        //如果比较器cpr不为null，即表明采用定制排序
        if (cpr != null) {
            do {
                //使用parent上次循环后的t所引用的Entry
                parent = t;
                 //将新插入的key和t的key进行比较
                cmp = cpr.compare(key, t.key);
                //如果新插入的key小于t的key，t等于t的左边节点
                if (cmp < 0)
                    t = t.left;
                //如果新插入的key大于t的key，t等于t的右边节点    
                else if (cmp > 0)
                    t = t.right;
                else
                //如果两个key相等，新value覆盖原有的value，并返回原有的value
                    return t.setValue(value);
            } while (t != null);
        }
        else {
            if (key == null)
                throw new NullPointerException();
            @SuppressWarnings("unchecked")
                Comparable<? super K> k = (Comparable<? super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        //将新插入的节点作为parent节点的子节点
        Entry<K,V> e = new Entry<>(key, value, parent);
        //如果新插入key小于parent的key,则e作为parent的左子节点
        if (cmp < 0)
            parent.left = e;
        //如果新插入key小于parent的key，则e作为parent的右子节点
        else
            parent.right = e;
        //修复红黑树
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }
//插入节点后修复红黑树
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;
​
    //直到x节点的父节点不是根，且x的父节点是红色
    while (x != null && x != root && x.parent.color == RED) {
        //如果x的父节点是其父节点的左子节点
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            //获取x的父节点的兄弟节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            //如果x的父节点的兄弟节点是红色
            if (colorOf(y) == RED) {     
                //将x的父节点设置为黑色
                setColor(parentOf(x), BLACK);
                //将x的父节点的兄弟节点设置为黑色
                setColor(y, BLACK);
                //将x的父节点的父节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            }
            //如果x的父节点的兄弟节点是黑色
            else {   
                //TODO 对应情况第二种，左右节点旋转
                //如果x是其父节点的右子节点
                if (x == rightOf(parentOf(x))) {
                    //将x的父节点设为x
                    x = parentOf(x);
                    //右旋转
                    rotateLeft(x);
                }
                //把x的父节点设置为黑色
                setColor(parentOf(x), BLACK);
                //把x的父节点父节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        }
        //如果x的父节点是其父节点的右子节点
        else {
            //获取x的父节点的兄弟节点
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            //只着色的情况对应的是最开始例子，没有旋转操作，但是要对应多次变换
            //如果x的父节点的兄弟节点是红色  
            if (colorOf(y) == RED) {
                //将x的父节点设置为黑色
                setColor(parentOf(x), BLACK);
                //将x的父节点的兄弟节点设为黑色
                setColor(y, BLACK);
                //将X的父节点的父节点（G）设置红色
                setColor(parentOf(parentOf(x)), RED);
                //将x设为x的父节点的节点
                x = parentOf(parentOf(x));
            }
            //如果x的父节点的兄弟节点是黑色
            else {
                //如果x是其父节点的左子节点
                if (x == leftOf(parentOf(x))) {
                    //将x的父节点设为x
                    x = parentOf(x);
                    //右旋转
                    rotateRight(x);
                }
                //将x的父节点设为黑色
                setColor(parentOf(x), BLACK);
                //把x的父节点的父节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    //将根节点强制设置为黑色
    root.color = BLACK;
}

TreeMap的插入节点和普通的排序二叉树没啥区别 , 唯一不同的是 , 在TreeMap插入节点后会调用方法fixAfterInsertion(e)来重新调整红黑树的结构来让红黑树保持平衡。

我们重点关注下红黑树的fixAfterInsertion(e)方法 , 接下来我们来分别介绍两种场景来演示fixAfterInsertion(e)方法的执行流程。

2.3.3.1 第一种场景: 只需变色即可平衡

同样是拿这颗红黑树举例，现在我们插入节点51。

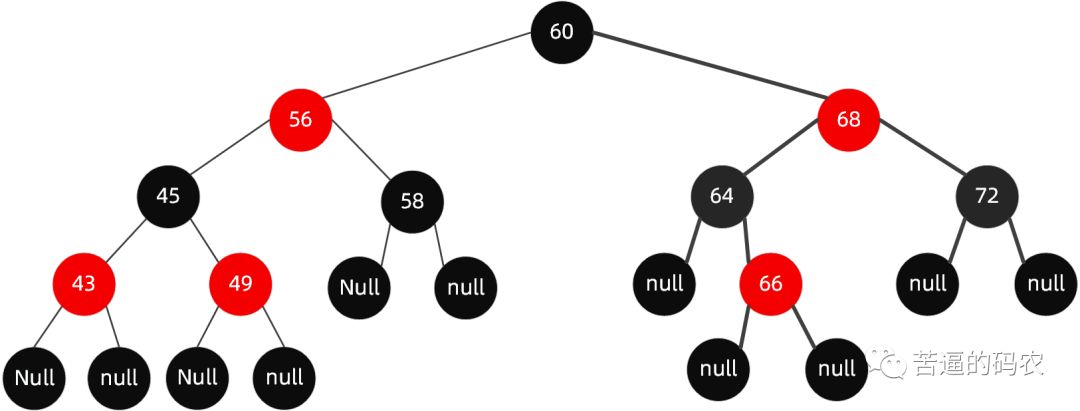
当我们需要插入节点51的时候 , 这个时候TreeMap的put方法执行后会得到下面这张图。

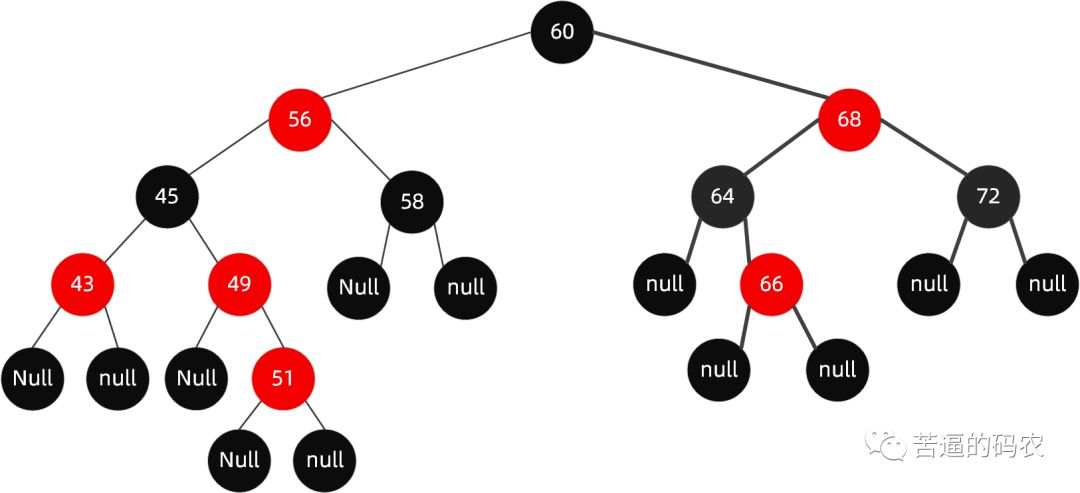
接着调用fixAfterInsertion(e)方法 , 如下代码流程所示。

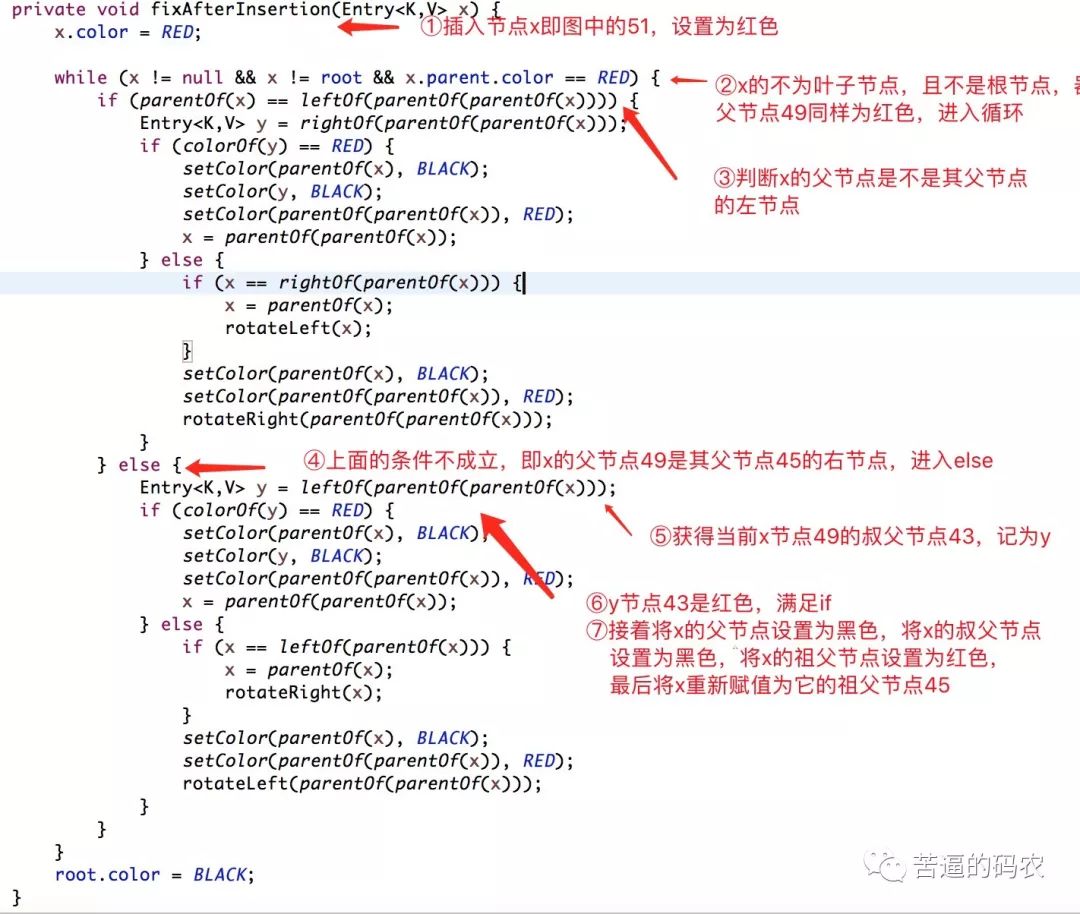
当第一次进入循环后 , 执行后会得到下面的红黑树结构。

在把 x重新赋值后 , 重新进入while循环 , 此时的x节点为45 。

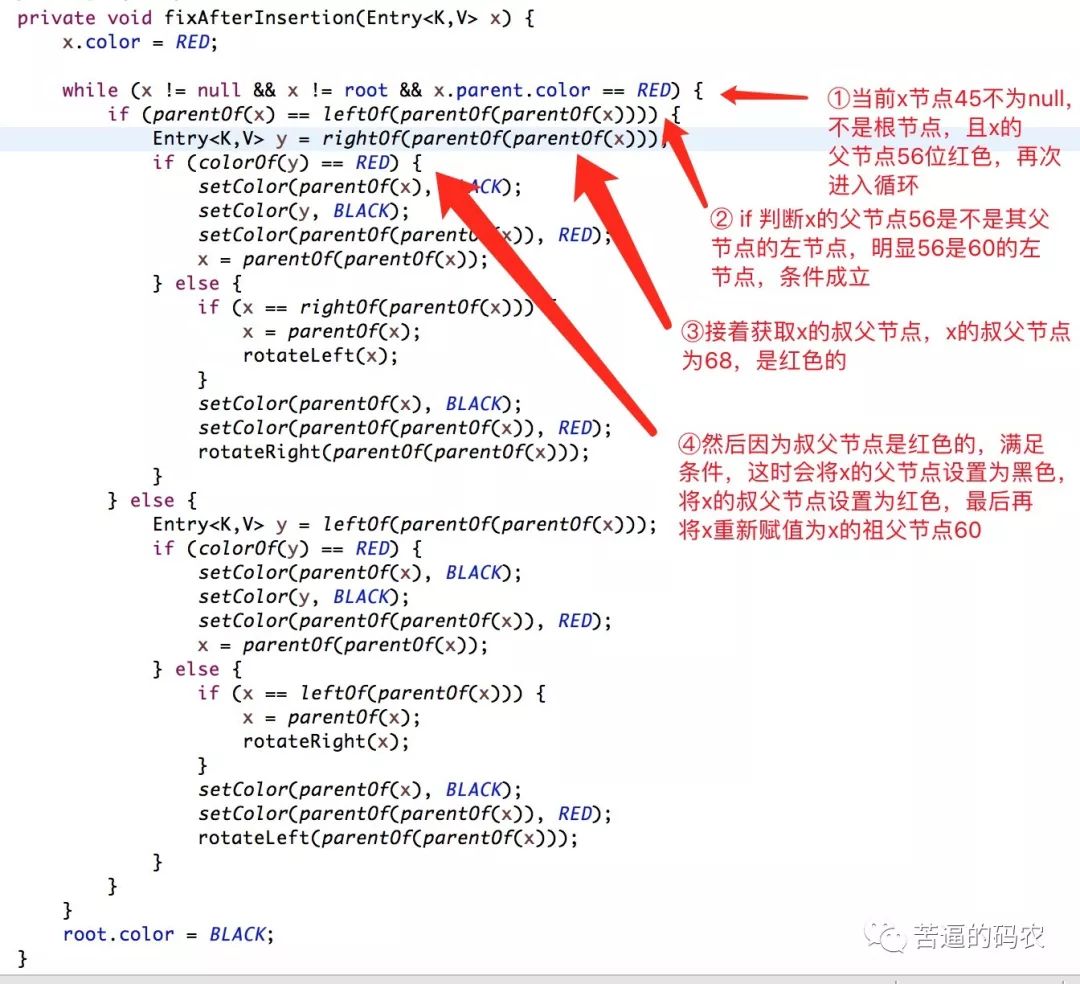
执行上述流程后 , 得到下面所示的红黑树结构。

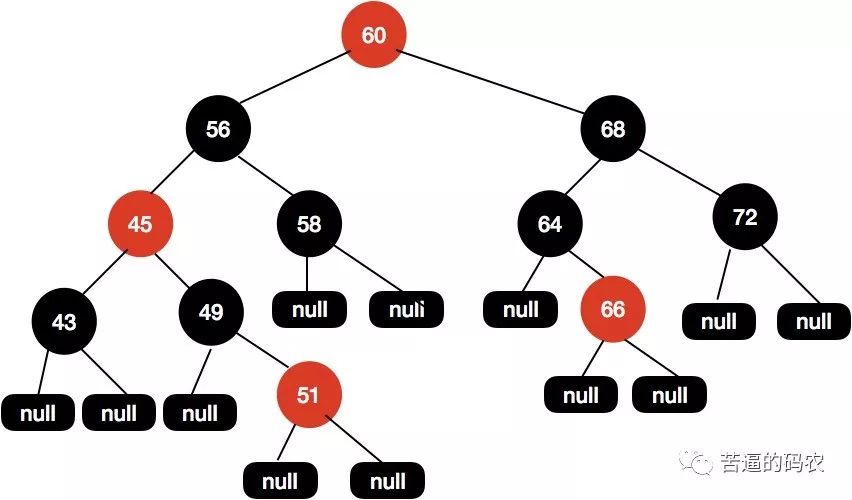
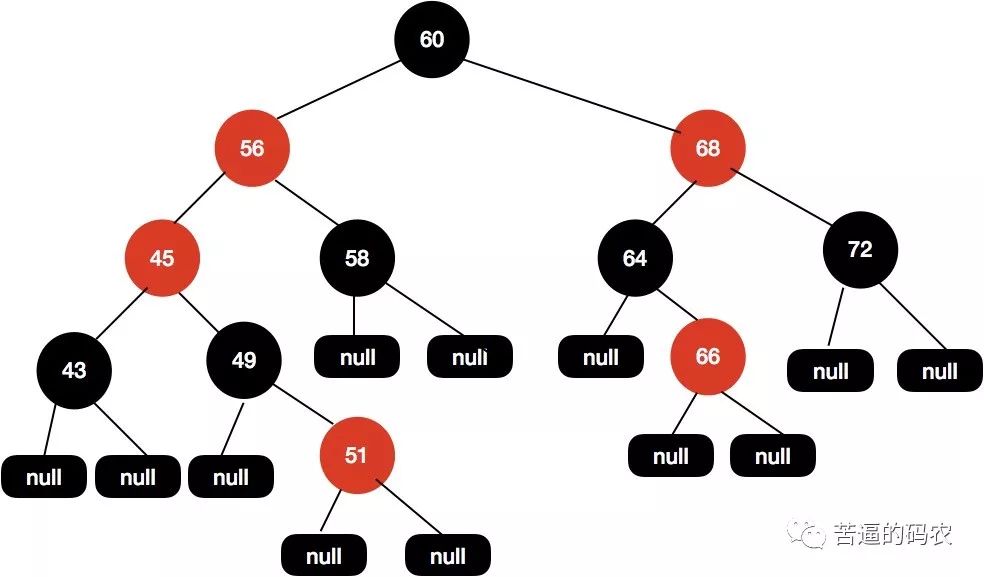
这个时候x被重新赋值为60 , 因为60是根节点 , 所以会退出while循环。在退出循序后 , 会再次把根节点设置为黑色 , 得到最终的结构如下图所示。

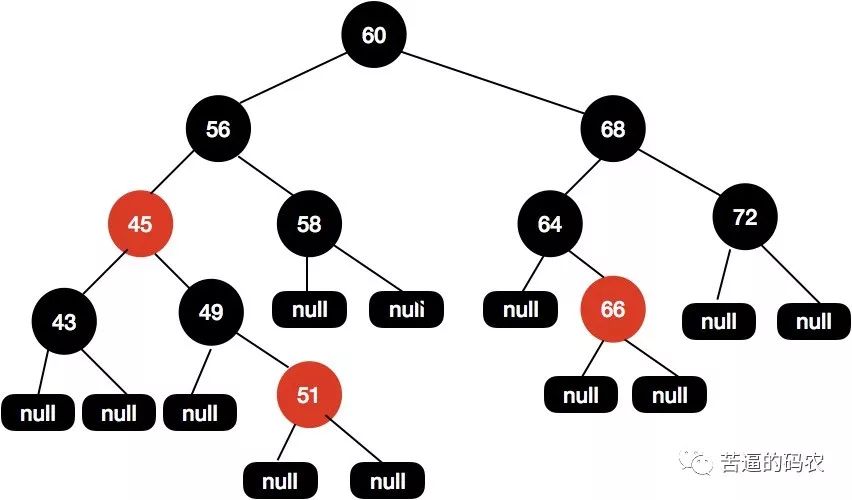
最后经过两次执行while循环后 , 我们的红黑树会调整成现在这样的结构 , 这样的红黑树结构是平衡的，所以路径的黑高一致，并且没有红色节点相连的情况。

2.3.3.2 第二种场景: 旋转搭配变色来保持平衡

接下来我们再来演示第二种场景 , 需要结合变色和旋转一起来保持平衡。

给定下面这样一颗红黑树:

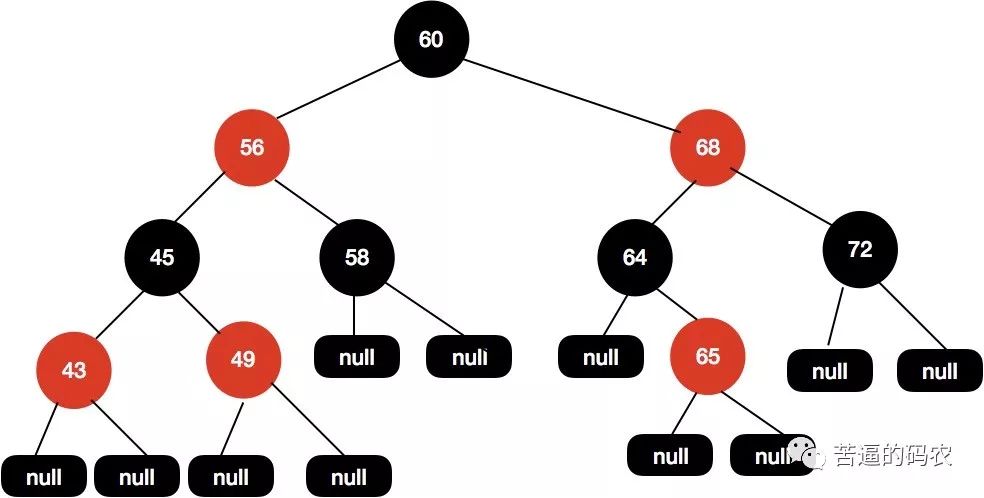
现在我们插入节点66 , 得到如下树结构。

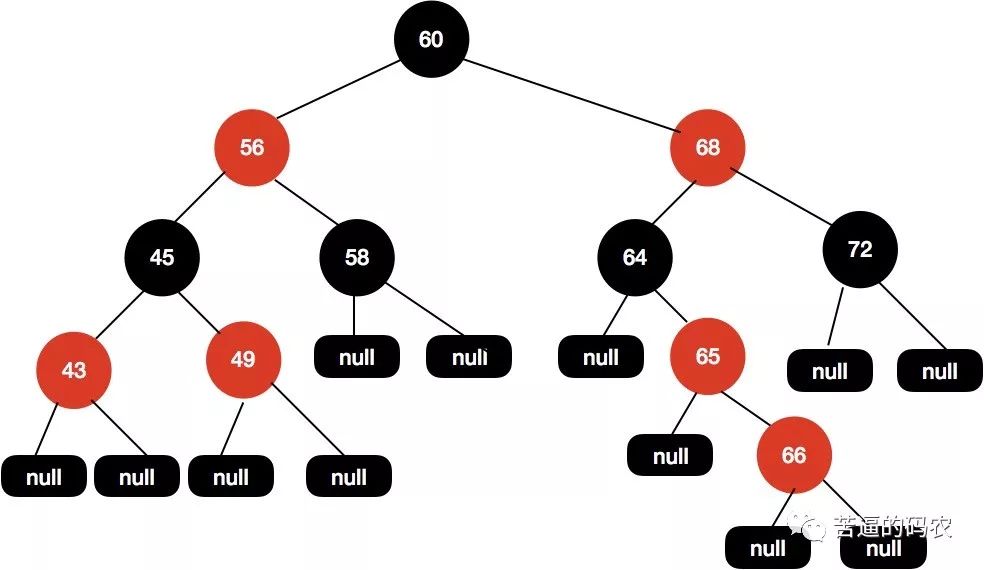
同样地 , 我们进入fixAfterInsertion(e)方法。

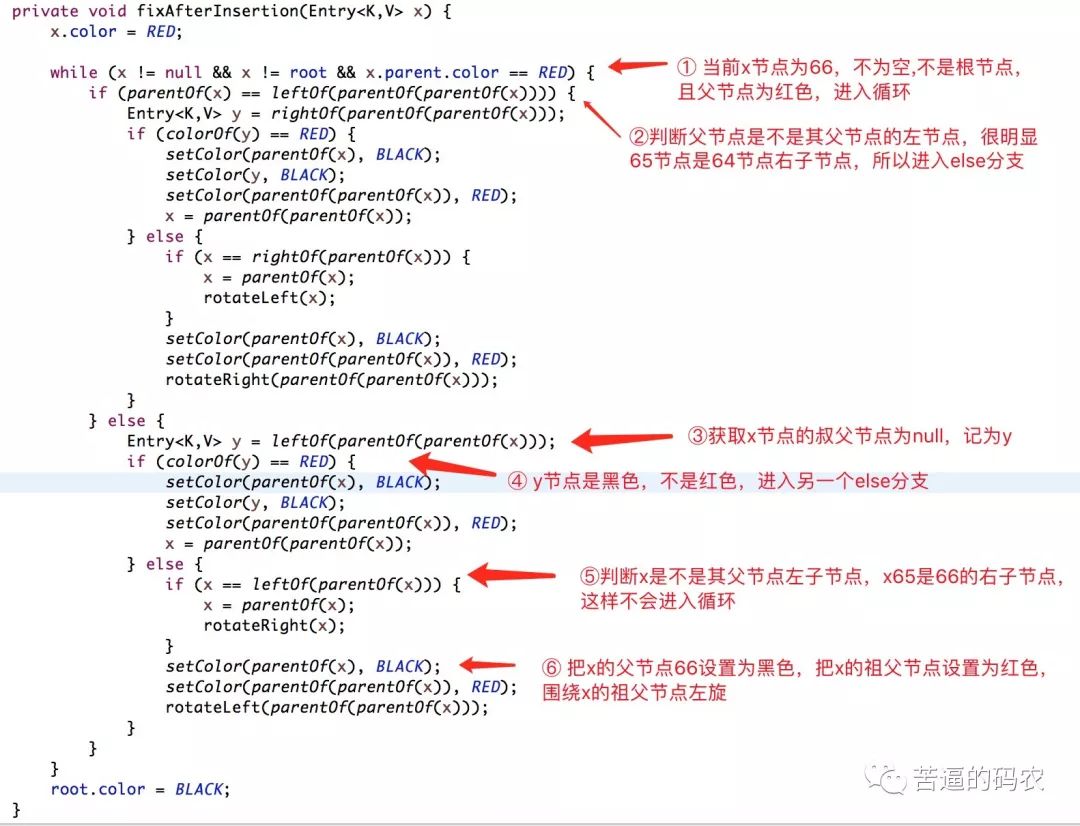
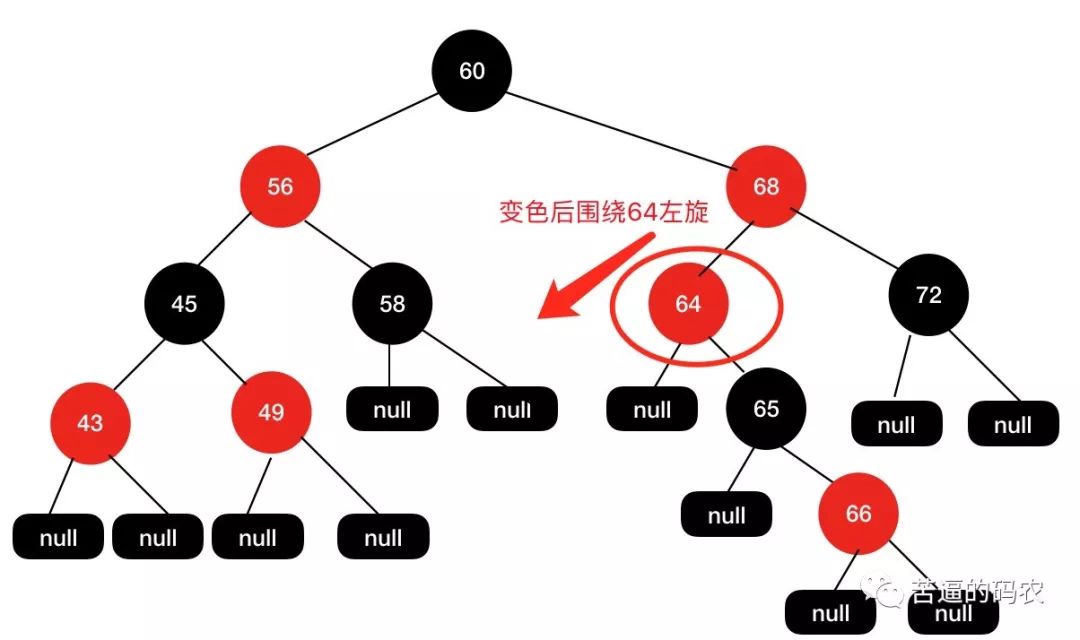
最终我们得到的红黑树结构如下图所示:

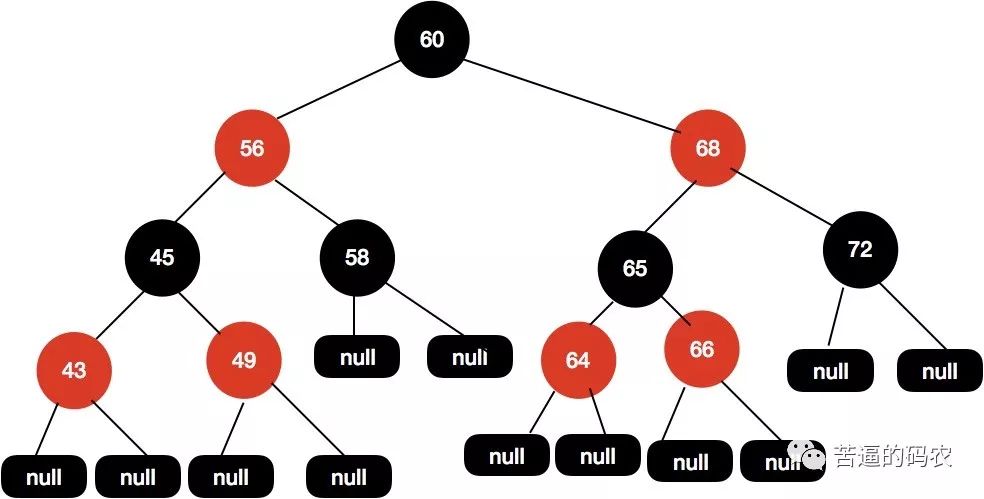
调整成这样的结构我们的红黑树又再次保持平衡了。

演示TreeMap的流程就拿这两种场景举例了 , 其他的就不一一举例了。

2.3.4 红黑树的删除

因为之前的分享只整理了红黑树的插入部分 , 本来想着红黑树的删除就不整理了 , 有人跟我反馈说红黑树的删除相对更复杂 , 于是索性还是把红黑树的删除再整理下。

删除相对插入来说 , 的确是要复杂一点 , 但是复杂的地方是因为在删除节点的这个操作情况有很多种 , 但是插入不一样 , 插入节点的时候实际上这个节点的位置是确定的 , 在节点插入成功后只需要调整红黑树的平衡就可以了。

但是删除不一样的是 , 删除节点的时候我们不能简单地把这个节点设置为null , 因为如果这个节点有子节点的情况下 , 不能简单地把当前删除的节点设置为null , 这个被删除的节点的位置需要有新的节点来填补。这样一来 , 需要分多种情况来处理了。

1. 删除节点是根节点

   直接删除根节点即可。

2. 删掉节点的左子节点和右子节点都是为空

   直接删除当前节点即可。

3. 删除节点有一个子节点不为空

   这个时候需要使用子节点来代替当前需要删除的节点 , 然后再把子节点删除即可。

   给定下面这棵树 , 当我们需要删除节点69的时候。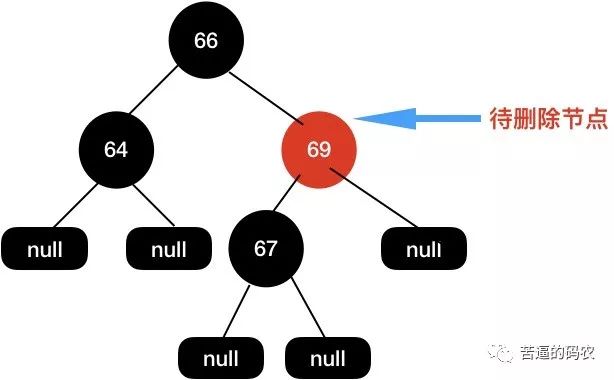

   

   首先用子节点代替当前待删除节点 , 然后再把子节点删除。

   

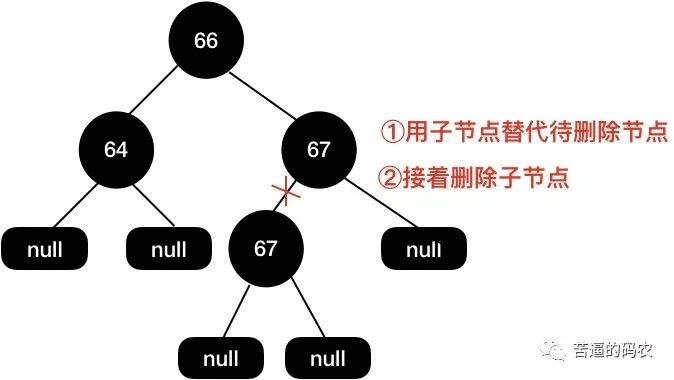
   最终的红黑树结构如下面所示 , 这个结构的红黑树我们是不需要通过变色+旋转来保持红黑树的平衡了 , 因为将子节点删除后树已经是平衡的了。

   

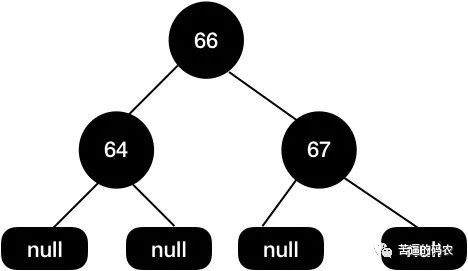
   还有一种场景是当我们待删除节点是黑色的 , 黑色的节点被删除后 , 树的黑高就会出现不一致的情况 , 这个时候就需要重新调整结构。

   还是拿上面这颗删除节点后的红黑树举例 , 我们现在需要删除节点67。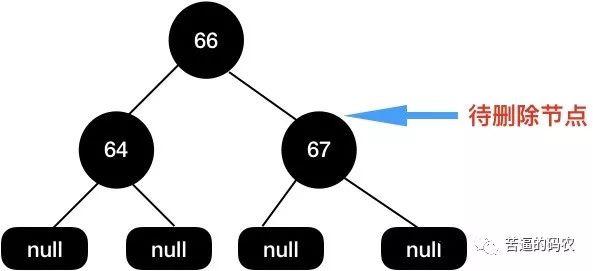

   

   因为67这个节点的两个子节点都是null , 所以直接删除,得到如下图所示结构: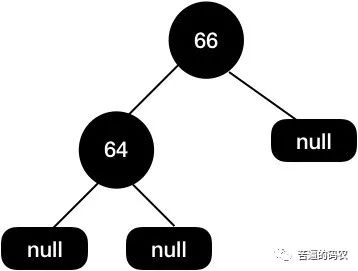

   

   这个时候我们树的黑高是不一致的 , 左边黑高是3 , 右边是2 , 所以我们需要把64节点设置为红色来保持平衡。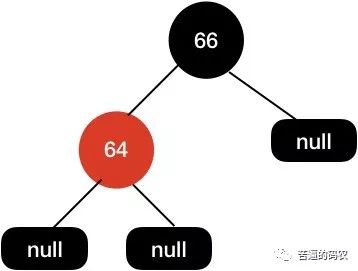

   

删除节点两个子节点都不为空

删除节点两个子节点都不为空的情况下 , 跟上面有一个节点不为空的情况下也是有点类似 , 同样是需要找能替代当前节点的节点 , 找到后 , 把能替代删除节点值复制过来 , 然后再把替代节点删除掉。

• 先找到替代节点 , 也就是前驱节点或者后继节点

• 然后把前驱节点或者后继节点复制到当前待删除节点的位置 , 然后在删除前驱节点或者后继节点。

那么什么叫做前驱，什么叫做后继呢？ 前驱是左子树中最大的节点 , 后继则是右子树中最小的节点。

前驱或者后继都是最接近当前节点的节点 , 当我们需要删除当前节点的时候 , 也就是找到能替代当前节点的节点 , 能够替代当前节点肯定是最接近当前节点。

在当前删除节点两个子节点不为空的场景下 , 我们需要再进行细分 , 主要分为以下三种情况。

第一种，前驱节点为黑色节点，同时有一个非空节点

如下面这样一棵树 , 我们需要删除节点64 :

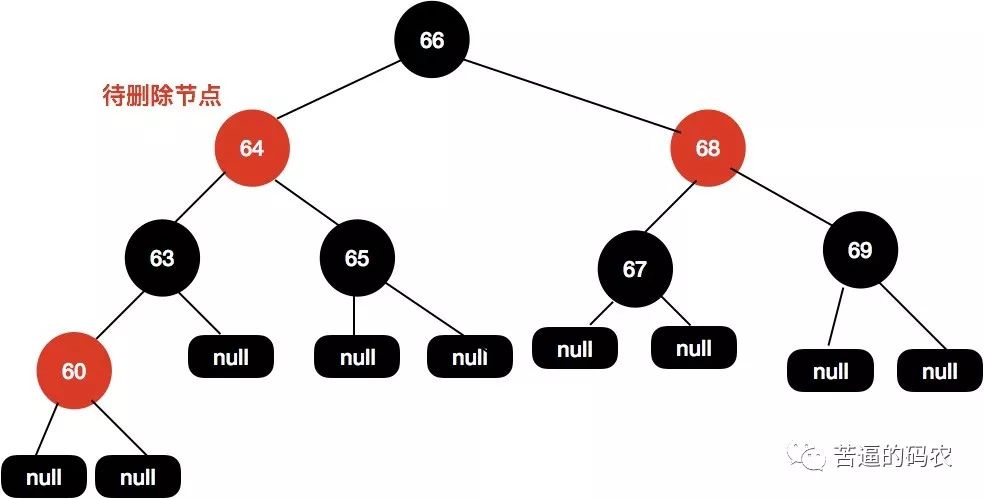
首先找到前驱节点 , 把前驱节点复制到当前节点:

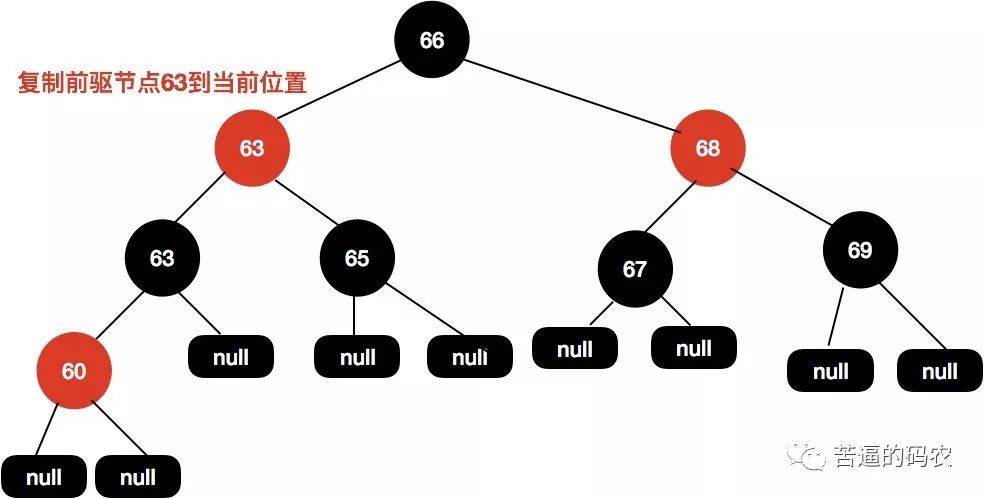
接着删除前驱节点。

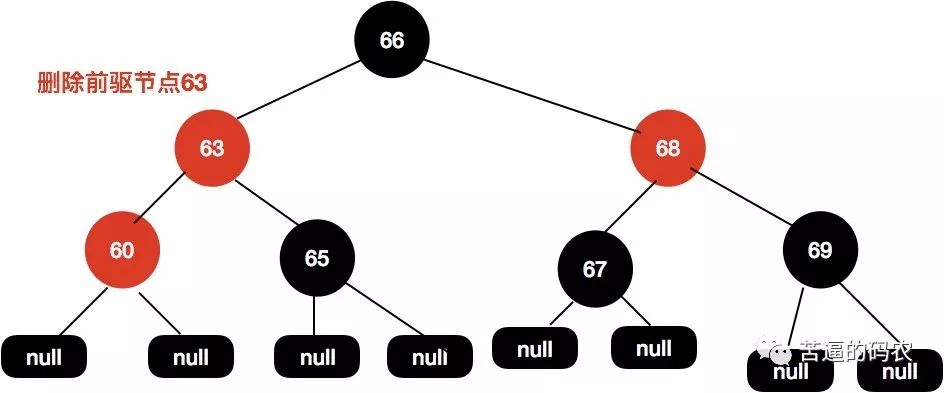
这个时候63和60这个节点都是红色的 , 我们尝试把60这个节点设置为红色即可使整个红黑树达到平衡。

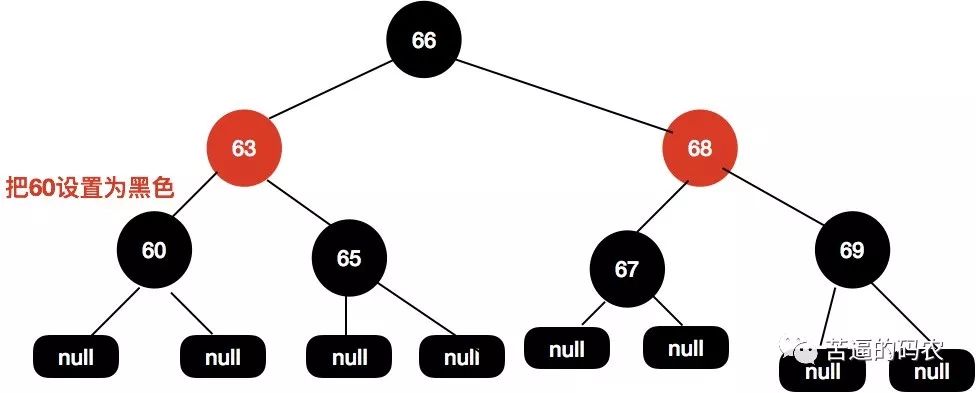
• 第二种 , 前驱节点为黑色节点，同时子节点都为空

  前驱节点是黑色的 , 子节点都为空 , 这个时候操作步骤与上面基本类似。

  如下操作步骤:

  

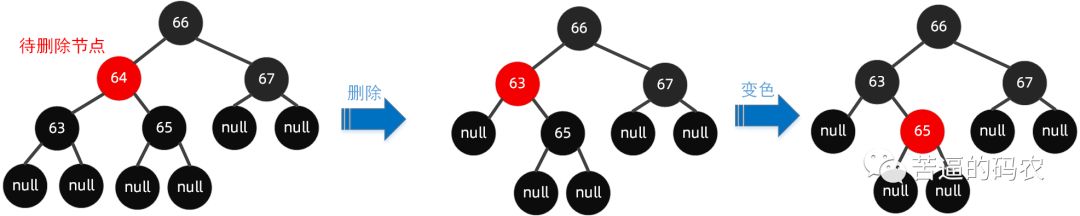
  因为要删除节点64 , 接着找到前驱节点63 , 把63节点复制到当前位置 , 然后将前驱节点63删除掉 , 变色后出现黑高不一致的情况下 , 最后把63节点设置为黑色 , 把65节点设置为红色 , 这样就能保证红黑树的平衡。

• 第三种，前驱节点为红色节点，同时子节点都为空

  给定下面这颗红黑树 , 我们需要删除节点64的时候。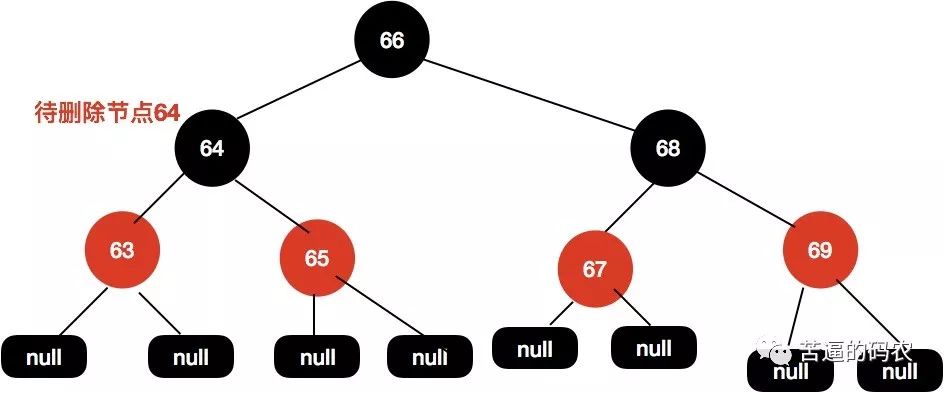

  

  同样地 , 我们找到64的前驱节点63 , 接着把63赋值到64这个位置。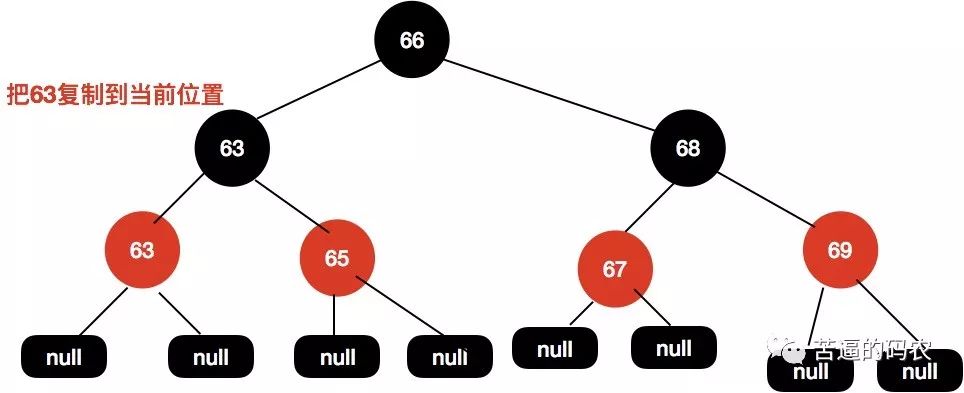

  

  然后删除前驱节点。

  

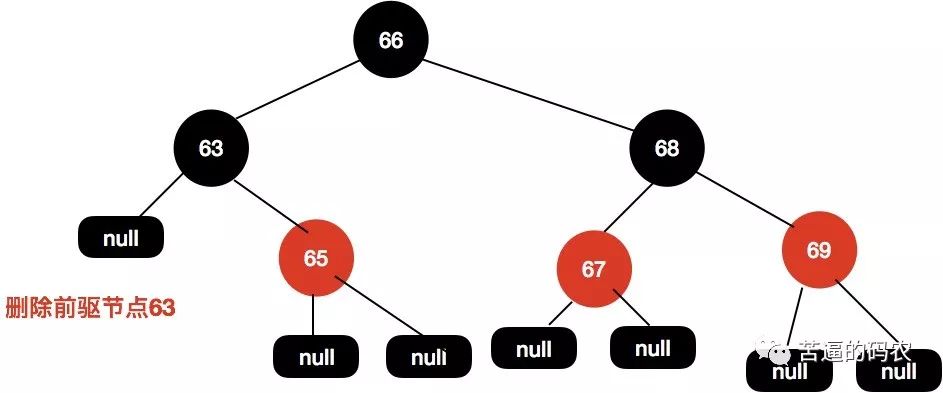
  删除节点后不需要变色也不需要旋转即可保持树的平衡。

2.4 满二叉树

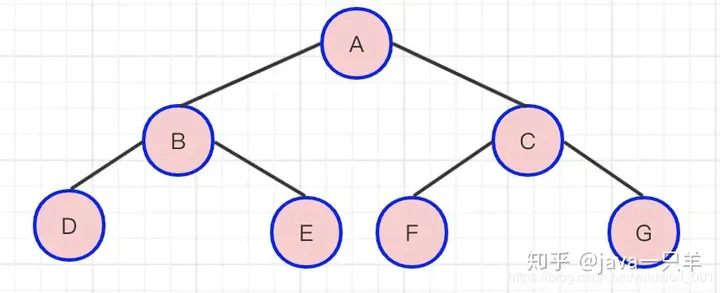
满二叉树 : 在一棵二叉树中。如果所有分支结点都存在左子树和右子树 , 并且所有叶子都在同一层上 , 这样的二叉树称为满二叉树。

满二叉树的特点有：

1. 满二叉树中第i层的节点数为 2^{i-1}个。

2. 深度为k的满二叉树必有 2^k-1个节点 , 叶子数为 2^{k-1}。非叶子结点的度一定是2。

3. 满二叉树中不存在度为1的节点 , 每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。叶子只能出现在最下一层。出现在其它层就不可能达成平衡。

4. 具有n个节点的满二叉树的深度为 log_2^{(n+1)}。

2.5 完全二叉树

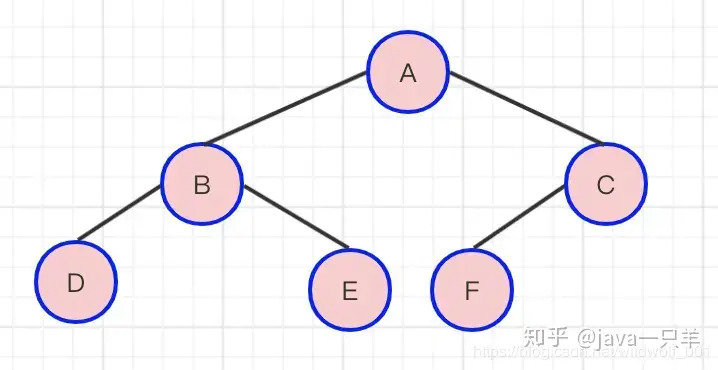
完全二叉树 : 对一颗具有n个结点的二叉树按层编号 , 如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同 , 则这棵二叉树称为完全二叉树。

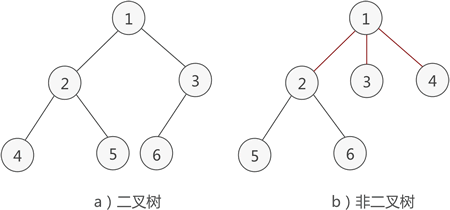
如图 a) 所示是一棵完全二叉树，图 b) 由于最后一层的节点没有按照从左向右分布，因此只能算作是普通的二叉树。

特点

1. 叶子结点只能出现在最下层和次下层。

2. 最下层的叶子结点集中在树的左部。

3. 倒数第二层若存在叶子结点，一定在右部连续位置。

4. 如果结点度为1 ,则该结点只有左孩子，即没有右子树。

5. 同样结点数目的二叉树 , 完全二叉树深度最小。

6. 满二叉树一定是完全二叉树，但反过来不一定成立。

完全二叉树除了具有普通二叉树的性质 , 它自身也具有一些独特的性质 , 比如说 , n个结点的完全二叉树的深度为 [log_2n]+1 , [log_2n]向下取整。例如 ,[log_24] = 2，而 [log_25] 结果也是 2。

对于任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号(如图 a)） , 对于任意一个结点i , 完全二叉树还有以下几个结论成立：

1. 当i>1时 , 父亲结点为结点[i/2]。(i=1时 , 表示的是根结点 , 无父亲结点)

2. 如果 2*i>n(总结点的个数) , 则结点i肯定没有左孩子(为叶子结点) ; 否则其左孩子是结点2*i 。

3. 如果 2*i+1>n , 则结点i肯定没有右孩子 ; 否则右孩子是结点2*i+1 。

3 二叉树遍历

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点 , 并且结点的存储位置 , 就是数组的下标索引。

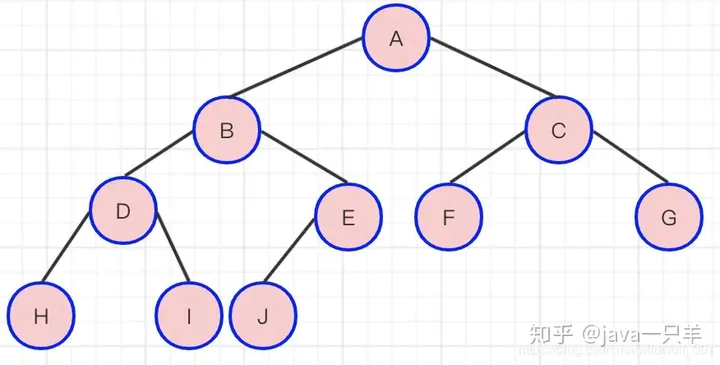
如图一棵完全二叉树按照顺序存储:

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。

访问次序

二叉树的访问次序可以分为四种：

1. 前序遍历 : 根结点 > 左子树 > 右子树

2. 中序遍历 : 左子树> 根结点 > 右子树

3. 后序遍历 : 左子树 > 右子树 > 根结点

4. 层序遍历 : 仅仅需按层次遍历就可以

3.1 前序遍历

前序遍历通俗的说就是从二叉树的根结点出发 , 当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。

遍历流程

1. 从根结点出发 , 则第一次到达结点A , 故输出A ;

2. 继续向左访问 , 第一次访问结点B , 故输出B ;

3. 按照同样规则 , 输出D , 输出H ;

4. 当到达叶子结点H , 返回到D , 此时已经是第二次到达D , 故不在输出D , 进而向D右子树访问 , D右子树不为空 , 则访问至I , 第一次到达I , 则输出I ;

5. I为叶子结点 , 则返回到D , D左右子树已经访问完毕 , 则返回到B , 进而到B右子树 , 第一次到达E , 故输出E ;

6. 向E左子树 , 故输出J ;

7. 按照同样的访问规则 , 继续输出C、F、G ;

前序遍历输出为：ABDHIEJCFG

3.2 中序遍历

中序遍历就是从二叉树的根结点出发 , 当第二次到达结点时就输出结点数据 ,按照先向左在向右的方向访问。

遍历流程

1. 从根结点出发 , 则第一次到达结点A , 不输出A , 继续向左访问 , 第一次访问结点B , 不输出B ;继续到达D ,H ;

2. 到达H , H左子树为空 , 则返回到H , 此时第二次访问H , 故输出H ;

3. H右子树为空 , 则返回至D , 此时第二次到达D , 故输出D ;

4. 由D返回至B , 第二次到达B , 故输出B ;

5. 按照同样规则继续访问 , 输出J、E、A、F、C、G ;

中序遍历输出为：HDIBJEAFCG

3.3后序遍历

后序遍历就是从二叉树的根结点出发 , 当第三次到达结点时就输出结点数据 , 按照先向左在向右的方向访问。

遍历流程

1. 从根结点出发 , 则第一次到达结点A , 不输出A , 继续向左访问 , 第一次访问结点B , 不输出B ; 继续到达D,H ;

2. 到达H , H左子树为空 , 则返回到H , 此时第二次访问H , 不输出H ;

3. H右子树为空 , 则返回至H , 此时第三次到达H , 故输出H ;

4. 由H返回至D , 第二次到达D , 不输出D ;

5. 继续访问至I , I左右子树均为空 , 故第三次访问I时 , 输出I ;

6. 返回至D , 此时第三次到达D , 故输出D ;

7. 按照同样规则继续访问 , 输出J、E、B、F、G、C 、A ;

后序遍历输出为：HIDJEBFGCA

3.4 层次遍历

层次遍历就是按照树的层次自上而下的遍历二叉树。

层次遍历输出为：ABCDEFGHIJ

参考链接

详解什么是平衡二叉树（AVL）（修订补充版） (qq.com)

动画 | 什么是红黑树？ (qq.com)

Mysql索引底层原理（一）(二叉树、红黑树、B树、B+树)_Java技术大联盟的博客-CSDN博客

MySQL 6种索引数据结构详解:BTree、B+Tree、红黑树、平衡二叉树、二叉树、Hash (qq.com)

数据结构之MySQL独爱B+树(二叉树、AVL树、红黑树、B树对比) | Laravel China 社区 (learnku.com)

图解：什么是红黑树？ - 知乎 (zhihu.com)

MySQL索引数据结构红黑树，Hash，B+树详解 - 风止雨歇 - 博客园 (cnblogs.com)